tempo, musical structure and the timing of grace notes
in skilled musical performance
Department of Music, University of Leeds, UK
Rinus Aarts, Peter Desain, Hank Heijink and Renee Timmers
NICI, University of Nijmegen, The Netherlands
Abstract
An experiment is reported which investigates the relationship between musical structure, predictions from the performance practice literature, and the timing of 11 grace notes in 45 performances of a short Beethoven piano piece at a range of tempi. These performances were recorded and analyzed so as to extract timing measurements, and the pianist was interviewed to gain insights into his conscious performing strategies. Significant differences in the relative length of different grace notes were found: the two grace notes with a large descending pitch interval were played significantly longer than the others. Additionally, the grace notes were timed such that they did not ‘take time’ from the note they are nominally attached to, but from the preceding time interval. Close attention to the qualitative data provided by the pianist reveals that the relative timing of the grace notes is best explained by his efforts to mimic the motor constraints of vocalists and string players, and by his tacit avoidance of dissonant vertical relationships between melody and accompaniment. Both of these interpretative decisions are in line with an explicit decision to attempt to play the piece in a ‘song-like’ manner. Lastly, the data provided evidence against the notion that changes in overall tempo leave the relative proportion of adjacent events invariant. Grace notes with a longer mean duration tended to deviate significantly from proportional duration, whilst shorter grace notes were roughly invariant over tempo. In summary, the results suggest that, in addition to the performer’s grasp of musical structure, both overall tempo and subtle communicative issues play important and measurable roles in determining the timing of musical events.
Introduction
This paper focuses upon the execution of grace notes in musical performance and is an attempt to address both musicological and psychological issues related to their timing. Both musicology and psychology have recently shown an increasing concern with issues in musical performance (see e.g. Rink, 1995). Such an interest in performances is in refreshing contrast to the study of notated scores, and allows the study of many musical and psychological issues that cannot be addressed through analysis of notation alone.
Within musicology, the study of historical performance practices has become a central concern. Donington (1963), for example, traces different styles of performance in baroque and pre-baroque music. From performance treatises he deduces the interpretation and application of ornamental notes and describes expressive devices in early music, such as the choice of tempo, the interpretation of meter, pulse and rhythm, and the use of articulation and dynamics. He discusses the main factors that transform a static score into a dynamic performance. This transformation, he argues, is made on the grounds of musical analysis and historically and stylistically differentiated musical conventions, which are in turn based on music theoretical interpretations and historical performance treatises. Such writings have become more than just a scholarly concern. There has been a considerable growth in the application of such historical studies to contemporary performance practice. The increasing concern with the use of historically appropriate instrumentation and style of performance has a mutual relationship with the academic study of past performance practices.
From the perspective of psychology, musical performance is considered "a rich domain for the study of cognitive and motor skills" (Palmer, 1997: 116). The aim of many studies in this field is to develop psychological theories of skilled performance mechanisms by investigating the cognitive and motoric processes that influence and constrain music performance. The study of motor aspects of musical performance has led to strong hypotheses concerning time-keeping mechanisms and motor programs. It has been argued that the performance of music is co-ordinated by an internal clock or clocks and executed by a memorized motor program (see e.g. Shaffer, Clarke and Todd, 1985). This motor program contains representations of an intended action and processes that translate these into a movement sequence. It has also been suggested that further constraints upon the execution of such motoric patterns come from kinematic or physical sources (e.g. Todd, 1995; Clarke, 1995; also see Palmer, 1997, for a review).
Psychological studies of music performance have also suggested many ways of conceptualizing the mental representation of musical structures and their role in controlling and structuring temporal, dynamic and timbral variations in performances. The rationale here is the idea that a performance conveys the musician's conceptual interpretation of the musical composition. This interpretation completes what the notation of music leaves undecided, such as the precise timing of notes and their intensity, tone quality, articulation and intonation. The function of this interpretation can be seen as solving ambiguities in the composition, but also as a method of highlighting structural and emotional aspects of the music. Experimental research has shown that structural elements of music such as phrase boundaries (Shaffer and Todd, 1987; Gabrielsson, 1987; Palmer, 1989; Repp, 1990; 1992; Todd, 1992) or metrical pulses (Sloboda, 1983; Clarke, 1985) are marked by systematic changes in timing, articulation and/or dynamics. For example, a common finding is that inter-onset intervals between sequential events at the end of a phrase tend to be progressively lengthened relative to their notated score durations. Similarly, different musical voices in a performance are separated by systematic changes in timing asynchrony between nominally synchronous events. (Palmer, 1989; 1996).
One specific consequence of viewing skilled musical performance as a sub-domain of motor control research is that the issue of "proportional duration" becomes extremely important. A dominant idea in the study of motor control is the notion that the timing of a particular sequence of actions can be predicted by a generalized motor program with a variable parameter controlling the overall rate of production (see Gentner, 1987 for a review). In musical terms this would mean that for performances of the same piece at different tempi by the same performer the same proportions should be observed between successive time intervals between events (Repp, 1994). A piece would have a single motor program which is controlled by a timekeeper which can generate the specified movements at a range of tempi. A related idea is that a modulated timekeeper, the rate of which is controlled by a continuous function, controls the timing of individual events in a musical sequence. The shape of such a function, it has been suggested, approximates a curve, often expressed as a parabola, or a number of parabolas additively combined (see e.g. Todd, 1985; 1989; 1992; 1995; Kronman and Sundberg, 1987; Longuet-Higgins and Lisle, 1989; Feldman, Epstein and Richards, 1992; or Repp, 1992 for different versions of this idea). It might therefore be suggested that the timing of the sequential events in a musical performance would thus retain not only relational invariance at different tempi, but also that the durations observed at these different tempi might be predicted by applying a scaling factor to such a function. This idea can be thought of as a "tempo curve", which, for example, might be directly derived from the hierarchical structure of the music (e.g. Todd, 1985). If both of these hypotheses are correct, a single tempo curve and some scaling factor could predict the timing of sequential events in a musical performance at two different tempi.
However, there are some doubts as to whether proportional duration is maintained at different rates of production in a number of domains, although it is unclear how much this conflicts with the notion of generalized motor programs themselves (see e.g. Gentner, 1987). Within the domain of music, conflicting evidence has been obtained regarding proportional duration. Repp (1994) has claimed that, despite some evidence against precise relational invariance, "the major (cognitively controlled) temporal and dynamic features of a performance change roughly in proportion with tempo, whereas minor features tend to be governed by tempo-independent motoric constraints" (Repp, 1994: 269). Indeed, it has been shown that when musical materials are extremely simple, both variability and note durations interact significantly with tempo (Mackenzie and Van Eerd, 1990), suggesting that Repp is correct to ascribe some of the between tempo variance he finds to sensori-motor constraints. However, Repp (1995) has shown that in a perceptual task there may be an interaction between tempo and timing for subjects’ preference ratings in performances of two solo piano pieces. His results suggest that increases in tempo must be matched by decreases in relative timing variation for subjects to give equivalent aesthetic ratings of performances at different tempi. Moreover, in a study of a different piece, Desain and Honing (1994) deviations from proportional duration in relation to higher level constraints on motor behavior. They claim that as well as motoric influences upon timing, there may be a strong interaction between the structural function of a particular event and its changes of duration over different tempi: its scaling behavior. In other words, they claim that the durations of different events may not only scale differently with overall tempo, but that such differences might be predicted by a classification of events into different structural classes. They argue that this seriously undermines the plausibility of timing being generated from some form of tempo curve without taking into account categorical differences between different events (Desain and Honing, 1993; 1994).
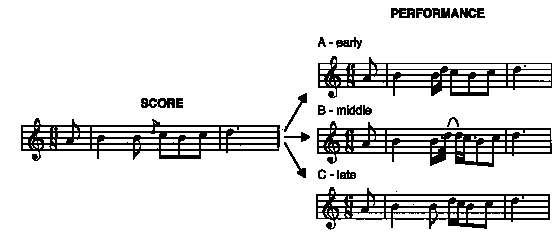
In this article a study will be reported that focuses on the timing of grace notes. Grace notes can be seen as additional notes that ornament or ‘flavor’ the melody and harmony, and can be omitted or added to a performance without fundamentally changing it. A grace note is notated as a small note before a regular note and its score duration is not precisely specified. The duration of grace notes is assumed to be subtracted from the following and/or previous note (see Figure 1). Note that throughout this paper all references to the duration of grace notes concern the inter-onset interval between the onset of a grace note and the following onset in the melody voice. This measure is taken to avoid a conflation of note-to-note timing with articulation. The sounding duration of a grace note may extend beyond the onset of the following note within the same voice, or the grace note may have an offset that occurs before this following onset. In this paper we will confine ourselves to onset-to-onset timing and will make no attempt to study the overlap between notes.

Hence, grace notes differ in many respects from regular notes, since they have no notated duration and interact with the durations of the notes that surround them. Therefore, they are especially interesting to study from both a musicological and psychological standpoint. What mechanisms determine the timing of grace notes? If the timing of individual events is generated from some form of tempo curve each event to be produced must have some form of score representation containing the canonical duration of that event. Todd, for example defines this as a "metrical grid" (Todd, 1995). There are no specified score durations for grace notes, and hence some investigation is necessary to attempt to discover the performed duration of grace notes relative to the performed durations of notes which have known score durations if one is to say anything concrete about their timing. Similarly, one might also ask how they scale over tempo in order to be able to predict not only their duration relative to a local musical context, but to do so for different tempi. Answering these questions will provide clues as to how grace note durations are controlled, and may also contribute to the modeling of expressive musical performance. One might also ask whether these aspects of grace note timing can be predicted by overall stylistic or historical factors, or from the specific musical context, and how independent these factors might be from sensori-motor constraints and timing variability. If grace notes vary in timing it is important to discover where this variability comes from, whether it is controlled, and whether such control reflects a representation of specific musical knowledge.
Previous research on the timing of grace notes has been inconclusive, except to show that like other aspects of musical timing, repeated performances of grace notes show some consistency (Repp, 1994; Desain & Honing, 1994). This supports the notion that grace notes are under considerable timing control. Whether such consistency exists equally between performances in different tempi, however remains unclear. Repp (1994) presents findings which support the notion of proportional duration over tempi for grace notes, although he notes that the grace notes in the piece used in his study may not be representative of more common types of grace notes. Desain and Honing (1994), however, find a considerable interaction between the duration of grace notes and tempo conditions. They even found that in one instance an increase in tempo was associated with an increase in the duration of a grace note, a rather surprising result. Moreover, they attempt to show that different types of grace notes, and the categories of rhythmic context in which they are embedded have different effects on their behavior over tempi. However, they do not directly test this hypothesis, and fail to account for the effect that variations in local tempo might have had on their data: it is possible, for instance, that although the overall tempi of two performances may be different, the local tempo around the location of two grace notes in the same position in the music might be the same, or even might vary in the opposite direction. This is especially true since they show that there is a strong interaction between tempo condition and the timing of individual events. A further shortcoming of this study is that only three tempo conditions were studied, making any claims about scaling behavior over a range of tempi difficult to substantiate in a detailed way. Nonetheless, this study suggests that by studying grace note timing one may be able to better investigate the relationship between local musical structure, timing and tempo.
There is further support from the musicological literature for the idea that the execution of grace notes cannot be explained without taking into account local musical structures, and even looking beyond these to stylistic and historical constraints. Neumann (1986:7-8,12), for example, claims that the execution of any ornament is highly dependent on the musical context in which it is situated. For him, the execution of ornaments can only be explained by making the harmonic, rhythmic and melodic function and the context of an ornament explicit and by defining the character, style and tempo of the piece.
Our study attempts to develop a better understanding of the production of grace notes by explicitly testing the relationship between different structural classifications of grace notes and their timing at different tempi. By collecting timing data from a musical context and analyzing the timing of grace notes that have different structural implications and are played at a wide range of different tempi, we will attempt to show that the local structure of music has a systematic effect on both the durations of grace notes and the relationship between these durations and local tempo measurements. In this way we hope to clarify the processes necessary to control timing in musical performance, and to show that the study of psychological processes in music can benefit from detailed attention to hypotheses drawn from the musicological literature. We also hope to demonstrate that systematic empirical work on timing can make a contribution to musical knowledge. We will do this by directly studying the links between scholarly research in performance practice and the actual practice of a skilled musician.
Method
Music
In this study we used the theme from Beethoven’s six variations in G-major WoO 70 (1795) on the duet "Nel cor più non mi sento" from the opera "La Molinara" by Giovanni Paisiello (see Appendix 1). The theme was chosen for its relative simplicity and brevity. It is especially suitable for this study as it contains 11 grace notes (numbered in square boxes in Appendix 1). Moreover, it is the same theme as was used in the study by Desain and Honing (1994), thus facilitating comparison with this earlier study.
The theme is 20 bars long, consisting of an initial 8-bar phrase, followed by a 6-bar phrase, and finishing with a 6-bar phrase. Although different structural interpretations are possible, the most straightforward phrase-structure tree is depicted in Figure 2.
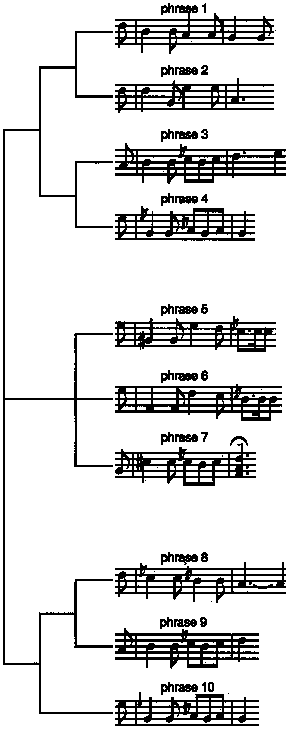
The first phrase consists of two subphrases that, in turn, can be divided into two further subphrases. The second phrase can be subdivided into three subphrases. The third phrase consists of two subphrases, of which the first subphrase is divided into two further subphrases. The theme has a typical Alberti Bass (broken-chord) accompaniment. All the grace notes are notated identically. Nevertheless, they can be separated and grouped on the basis of their musical function and context in the following ways:
In order to help formulate hypotheses based on structural differences between grace notes, they were classified into groups with similar features on the basis of:
A Melodic configuration:
Note repeat with descending sixth: 2, 10
Note repeat with descending second: 4, 5, 7, 8
Rising third, descending second: 1, 3, 9, 11
Rising second, descending second: 6
B Metrical position:
Strong beat: 2, 4, 5, 7, 10
Weak beat: 1, 3, 6, 8, 9, 11
C Rhythmic configuration following the grace note:
Three eighth notes 1, 3, 6, 9, 11
Dotted eighth note and eighth note 4, 5
Quarter and eighth note 2, 7, 8, 10
D Harmonic configuration:
Grace note is:
Dissonant 2, 4, 5, 6, 8, 10
Consonant non-chord tones 1, 3, 9, 11
Chord tone 7
E Phrase position:
Beginning of two bar phrase 2, 7, 10
Middle of two bar phrase 1, 3, 6, 8, 9, 11
End of two bar phrase 4, 5
F Position in greater metrical framework, or longer-term phrase structure
Relatively weak metrical level 1, 3, 6, 8, 9, 11
Intermediately strong metrical level 4, 5
Relatively strong metrical level 2, 7, 10
Support for most of these categorizations comes from Neumann (1978; 1986). We would like to advance a number of hypotheses in relation to these music-theoretical categorizations. First, we would expect that grace notes that occur in different categories would have different mean durations, regardless of tempo. Note for example that grace notes 2 and 10 always occur in the same category: we would predict that these would have a significantly different duration to the other grace notes. Second, we would predict that some of the structural categories above would encourage a relative lengthening of grace note duration for expressive purposes: some form of duration accent. The grace notes that would be lengthened would be in (A) the grace notes with a large descending interval (2 and 10); in (B) those on a strong beat (2, 4, 5, 7 and 10); in (C) those that precede a relatively long note (2, 7, 8 and 10); in (D) those that are dissonant (2, 4, 5, 6, 8, 10); in (E) those at the beginning of a phrase unit (2, 7 and10); and in (F), those that occur at a relatively strong metrical level (2, 7 and 10). Again, 2 and 10 always seem to be candidates that would be relatively long, since they occur only in categories in which we would predict lengthening.
It is hard to make any clear predictions regarding the changes in such timing over different tempi since the musicological literature provides no clues as to how such changes might occur. However, we would predict that, in accordance with Desain and Honing (1994), relational invariance will not hold, and that the relationship between timing and tempo will differ from grace note to grace note. Although we make no direct predictions regarding the position of each grace note in relation to the following note and to the accompaniment, we will attempt to see whether there is some consistent relationship between these three onsets.
Performer
A professional pianist, age 26, participated as subject in this experiment. He started taking classical piano lessons at the age of nine. He completed his studies at conservatory and has since played with several orchestras and chamber music ensembles. Currently he is a Professor of Piano at the Tilburg Conservatory in the Netherlands. The pianist was paid an appropriate fee for his services.
Procedure
Recordings were made in the "Music, Mind, Machine" laboratory on a Yamaha Disklavier MIDI grand piano. This instrument optically detects key velocities and pedal movements and converts this information to standard MIDI messages. The piano was connected by a MIDI cable to a Macintosh PowerPC 9600/233 microcomputer running Opcode Studio Vision Pro 3.5.4 (time resolution 1 ms, within the limits of MIDI transmission speed) under MacOS 8.1. An unobtrusive video-camera recorded the pianist during the experiment and the interview.
Upon arrival, the pianist was given time to accommodate and warm up. Three weeks prior to the experiment he had been asked to prepare performances of the theme at 9 different tempi, using the notation shown in Appendix 1, with the boxed numbers and direction "Thema (andantino)" removed, and told that he would have to perform the piece five times at each tempo. The nine different tempi were 50, 52, 55, 57, 60, 63, 67, 71, and 75 dotted quarter note beats per minute. These tempi were chosen because they span a reasonable range, yet are all within the bounds of technique and our musical taste. The pianist reported that although the more extreme tempi would not be his first choices, they were musically acceptable, especially after he had accustomed himself to them through practice.
Within the experiment the pianist was instructed to play a sequence of a block of five repetitions of the theme at each of the nine tempi giving a total of 45 complete performances. The order of the tempo blocks was random, and before each block of repetitions the pianist was told the required tempo by one of the experimenters. The pianist was then allowed to practice the theme at the tempo requested (a digital metronome was provided to remind the pianist of the tempo), and was asked to indicate whenever the next five repetitions could be recorded. Between each repetition there was a short break of about 5 seconds. No feedback was given as to whether the required tempo was maintained: he was just told to concentrate on keeping the tempo as close to the required tempo while playing as musically and naturally as possible, and not to hesitate too long between repetitions. The pianist was allowed to rest between tempo conditions, but needed only one short break.
The duration of the experiment was about one hour. After completion, the pianist was asked a few questions concerning the experiment and the theme, so as to gain more information about his insights into the task, view of the musical material, and interpretative choices. Following the experiment, the timing data were stored in standard MIDI files (MMA, 1996). These files were imported into POCO, a computer environment for research on expression in music (Honing, 1990). A robust performance-score-matching facility in POCO was used (Desain, Honing and Heijink, 1997). It transferred structural information from a score representation to the 45 performances, including the position of the grace notes, voicing, and metrical structure. At the same time, this procedure provided a secure check for performance errors. POCO was then used to extract timing measurements across performances, using this structural information to locate and measure the duration of the grace notes and other relevant events. Two statistical data-analysis programs (JMP 3.2.2 and Statview 4.5) were used for further processing and statistical analysis.
Results
To analyze the timing behavior of grace notes, the proportional inter-onset interval (IOI) of each grace note in every performance was measured. IOIs are used instead of durations, as is common in the analysis of timing in musical performance to avoid confounding timing and articulation. All IOIs in this paper are expressed in seconds. An IOI is the time elapsed between the onset of a note and the onset of the following note. It is possible to calculate the proportional IOI of a grace note by dividing it by the total duration of the performance. However, this will result in an unreliable measure, because tempo fluctuates during a performance. This can be seen in Figure 3, which shows the tempo per bar, averaged over all performances, expressed in dotted quarter note beats per minute.
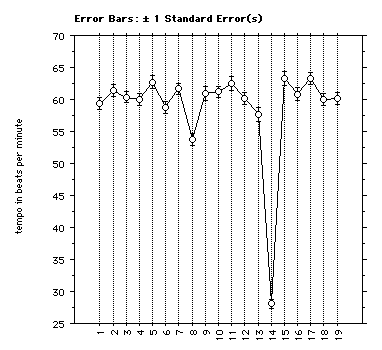
So, instead of taking the average duration of an 8th note over the whole piece, we will use the smallest possible time span to measure tempo, which is the average duration of an 8th note within the context of each grace note. The context of each grace note is the IOI between the onset of the note preceding the grace note and the onset of the note subsequent to the note that follows the grace note. The local 8th note IOI is the context IOI divided by the number of 8th note beats it contains. We now arrive at a proportional grace note IOI by dividing the grace note IOI by the local 8th note IOI. We will express this proportion as a percentage. For example, a proportional grace note IOI of 50% means that the grace note IOI is half as long as the local 8th note IOI.
To determine the effects of local tempo and grace note position on the length of the grace notes an ANCOVA was calculated with proportional grace note IOI as a dependent variable, local 8th note IOI as a covariate, grace note position as main effect (11 levels), and repetition (5 levels) as a random factor. There were significant main effects of position (F10, 469 = 2.2871, p = 0.0127) and local 8th note IOI (F1, 469 = 38.1755, p < 0.0001). Moreover there was a significant interaction between position and local 8th IOI (F10, 469 = 4.5418, p < 0.001). Note that repetition was not a significant effect (p = 0.5289): the pianist was clearly consistent within each tempo block. A more detailed analysis of each of the significant effects follows.
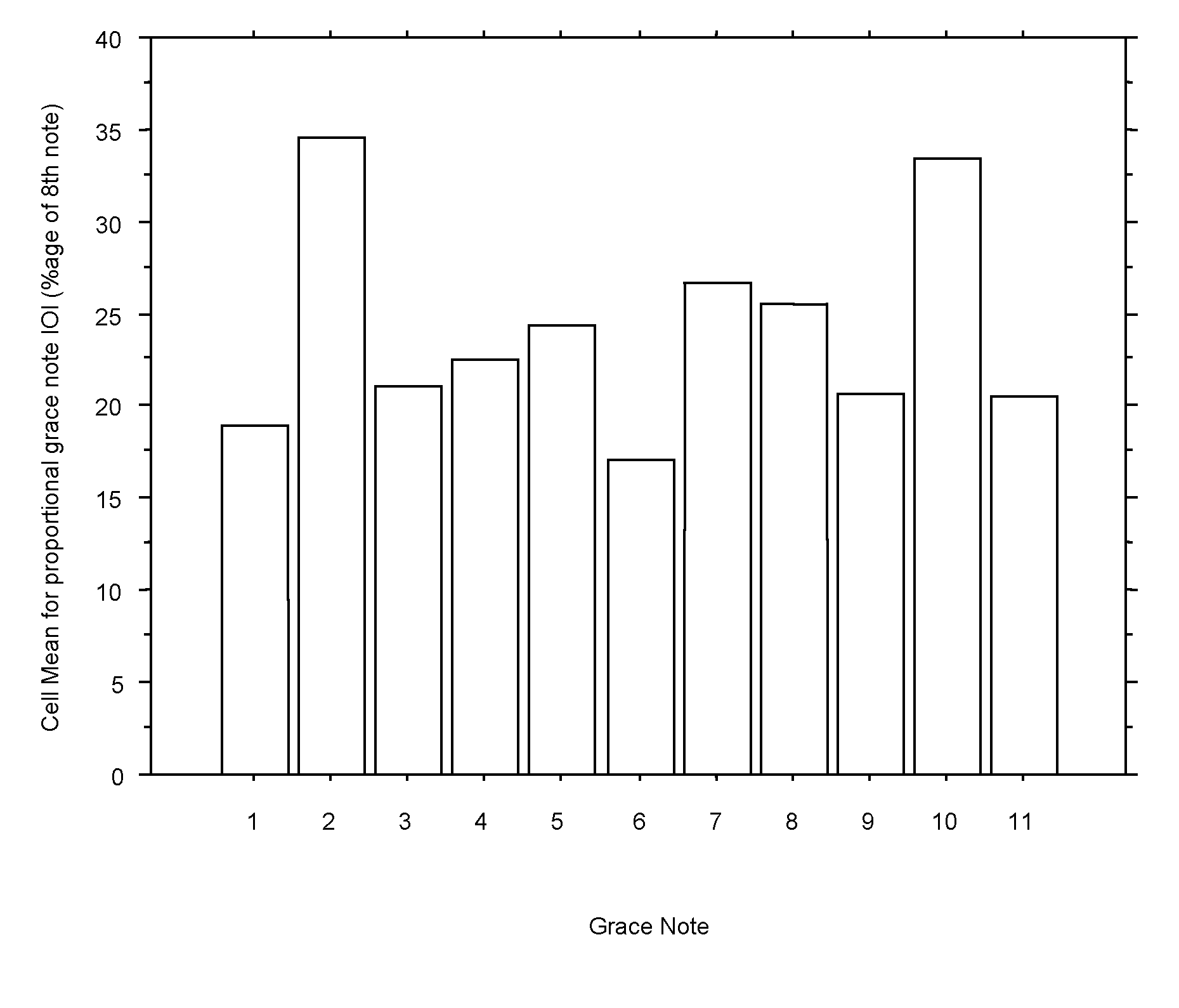
We will first focus on the effect of position on proportional grace note IOI. Figure 4 shows for each position the mean proportional grace note IOI. Grace notes 2 and 10 both have the largest average proportional IOI. A Tukey-Kramer mean comparison between all grace notes shows that only grace note 2 and 10 have means that are not significantly different from each other, but significantly different to all the other means (at a 0.05 significance level). We will offer an explanation of why these two grace notes should be played relatively long in the discussion section below.
Next, Figure 5 illustrates the effect of local 8th note IOI on proportional grace note IOI across all grace note positions and repetitions, taking proportional grace note IOI as the dependent variable and local 8th note IOI as the predictor. This is equivalent to the test for proportional invariance described in Gentner (1987). If the grace note IOIs were timed proportionally with changes in tempo one would expect a regression with a non-significant slope. This was not the case here: a small regression effect was found (R2 (494) = .104, p < .0001) with a significant positive slope. This means that the grace note IOIs are not relationally invariant with local 8th note IOI. As the local 8th note IOIs get longer, the grace note IOIs increase more than would be expected from a proportional duration model. In other words, when tempo decreases, the grace note IOIs slow down are lengthened more than notes in their surrounding context.
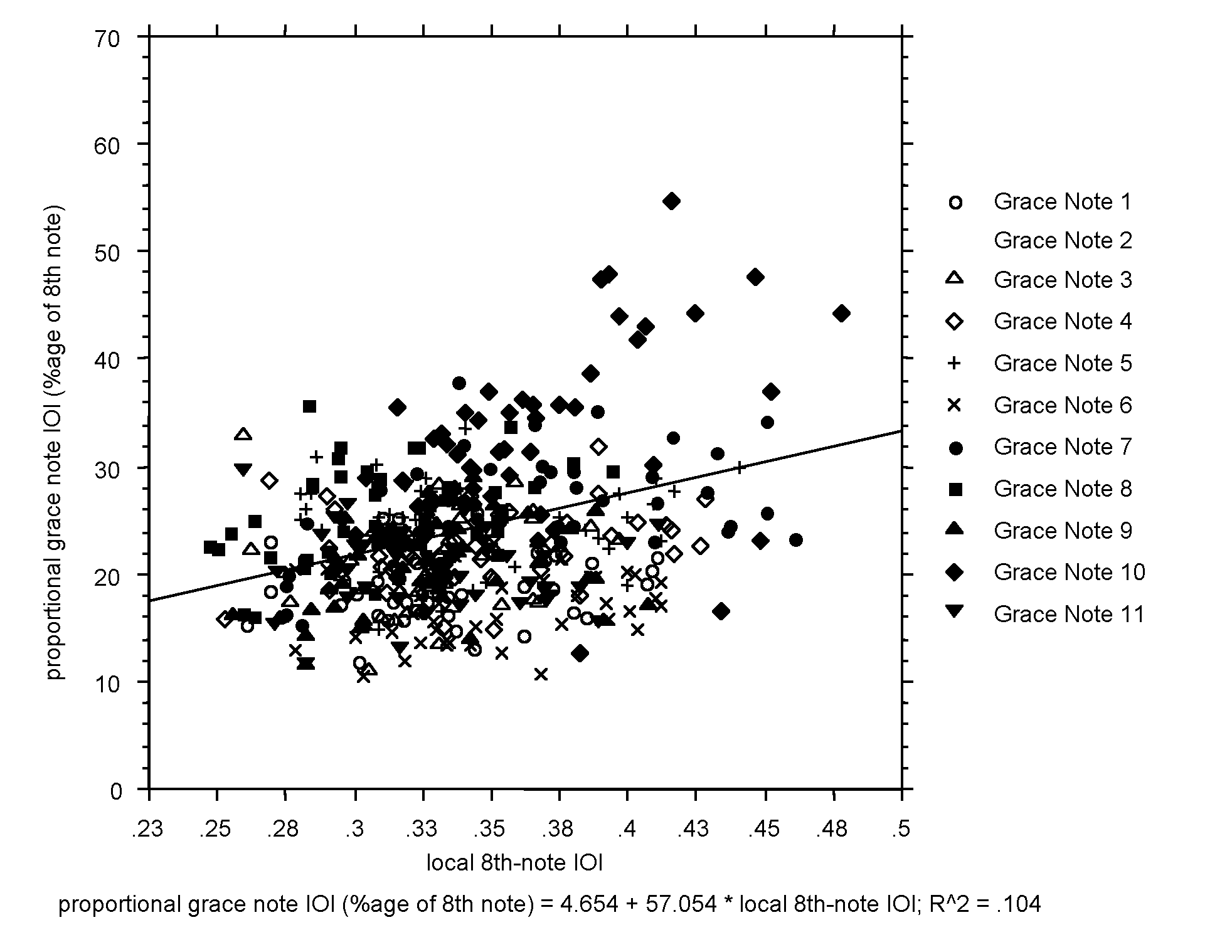
Along with the main effect of local 8th note IOI, there was a significant interaction between local 8th note IOI and grace note position on proportional grace note IOI. This means that the grace note IOI scaling behavior is different depending on the position of the grace note within the piece. Separate linear regressions were calculated between proportional grace note IOI and local 8th note IOI for each grace note position. The results are shown in Table 1. For grace notes 2, 7, 8, 9, and 10 a significant regression was found with a positive slope. For all other grace notes, the mean proportional IOI was the best predictor. This means that in only half the cases could anything like proportional duration be claimed, which is rather more than the 10% rejection rate required by Gentner (1987) for a series of tests of this kind.
Grace Note R squared p = Mean proportional IOI Regression Equation (Y = proportional grace note IOI; X =
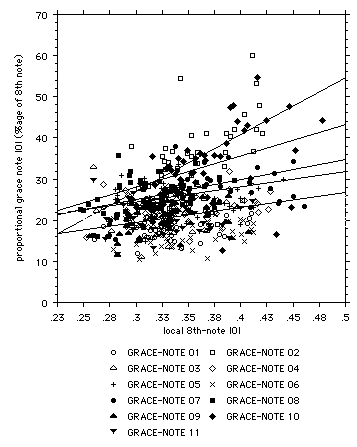
local 8th-note IOI) 1 0.01 n.s. .189 Y = .156 + .1 * X 2 0.33 < 0.0001 .346 Y = -.14 + 1.373 * X 3 0.007 n.s. .211 Y = .172 + .119 * X 4 0.07 n.s. .225 Y = .145 + .233 * X 5 0.006 n.s. .244 Y = .22 + .072 * X 6 0.04 n.s. .171 Y = .107 + .183 * X 7 0.17 0.005 .266 Y = .133 + .37 * X 8 0.14 0.01 .255 Y = .104 + .489 * X 9 0.09 0.04 .206 Y = .088 + .357 * X 10 0.14 0.01 .333 Y = .05 + .766 * X 11 0.01 n.s. .206 Y = .247 - .124 * X
The significant regression lines are plotted in Figure 6. Clearly, the slopes of the regressions associated with positions 2 and 10 are greater than those for the others, with 7 and 8 coming close behind. Position 9 is barely significant. Grace notes 2, 7, 8 and 10 also have the greatest mean proportional IOIs, suggesting either longer notes scale more than shorter ones, or that some underlying factor has an effect on both duration and scaling.
In order to describe the relative positioning of grace notes, we analyzed the onset of each grace note and its following melody note (hereafter: main note) relative to the onset of the accompaniment note (coinciding with the main note) over changing local 8th note IOI. Figure 7 shows the relative timing in seconds of the main note and grace note, taking the accompaniment note in the left-hand as a reference. Note onsets that occur before the accompaniment are negative; those following it are positive. Also plotted on the scattergram are regression lines for relative main note timing versus local 8th note IOI and relative grace note timing versus local 8th note IOI.
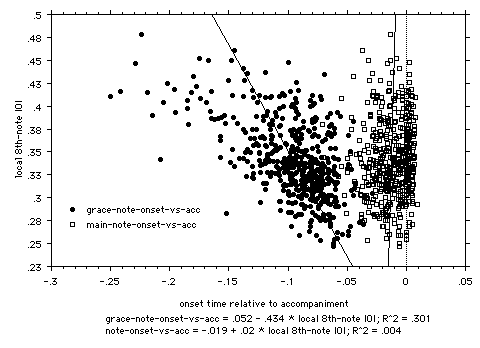
The increasing distance between the regression lines expresses the scaling of the IOIs with tempo. The relationship between main note and accompaniment note remains constant over tempo, with a mean asynchrony of 0.012 seconds: the regression is not significant. Therefore, the increase in grace note IOI does not create a corresponding increase in left-right hand asynchrony and the main note tends to lead the accompaniment across the range of local tempi. Moreover, the increasing duration between grace note and main note over tempo suggests that as the grace notes scale with tempo their onsets occur earlier relative to both main note and accompaniment note, rather than by displacing the onset of the main note later and later.
Discussion
There are four topics we would like to address here. We will argue that there are at least two different categories of grace notes, that the grace note IOI can be predicted partly from structural classifications of the grace notes, that relatively long grace notes scale differently over tempo to relatively short grace notes, and that there is a consistent relationship between grace note onset, main note onset and right-hand note onset. Of course, these findings apply to only one performer, to one piece and to one musical style. However, although this makes general claims problematic, we would like to stress that in this study a decision was made to obtain a detailed understanding of a single performer and piece through the collection and analysis of a relatively large dataset of repeated performances. Another performer might exhibit different patterns of timing, and our performer might well have performed a different piece or style of music in a rather different manner. The advantage of a single performer study of this kind is that more reliable conclusions may be drawn, by virtue of this large number of directly comparable measurements.
Our results show that grace notes 2 and 10 are consistently and significantly played longer than the other grace notes over all the different tempi. Our hypothesis regarding this effect was that grace notes in different music-theoretical categories would be played differently, regardless of tempo. Indeed, a classification by melodic configuration makes a separate category of grace notes 2 and 10. We found no evidence for the further categorization of grace notes preceding a descending second; only the interval directly following the grace note seems to be of importance. Desain and Honing (1994) suggest a classification of appogiature (grace notes 2 and 10) and accaciaturre (the others). Their classification is supported by our findings, although we would take issue with their application of these particular names (see below).
A different but related hypothesis is that the categories within a classification are differentiated by lengthening the grace notes in one category more than the grace notes in the other categories. The only classification that supports this hypothesis is melodic configuration, as we discussed in the previous paragraph. A classification by phrase position puts grace notes 2, 7 and 10 together. Grace note 7 is, however, not significantly longer than the other grace notes. Our findings do not support the hypothesis that any of the other classifications are differentiated by lengthening grace notes. We would, therefore, argue that melodic configuration and more particularly, the interval directly following the grace note, is predominant in determining the length of a grace note. Our pianist confirmed this in his comments after the experiment by saying "[grace notes] 2 and 10 are striking, because they span such a large interval. A singer or a cellist needs a lot of time to make that jump and [lengthening the grace notes] makes the grace notes more expressive." Our findings are particularly striking in the light of these comments. Although there is no technical reason for the pianist to lengthen these particular intervals, he consciously aims to do so in order to mimic the technical constraints other musical instruments entail. The pianist's execution of these intervals is not, as far as we can see, limited by motoric factors, but by an interpretative decision based on a desire to mimic other instruments. It should be noted that the original melody was intended as a vocal piece: we might speculate that, in this case, the pianist is attempting to evoke this provenance in his interpretation. In other words, a technical constraint on one instrument is in this case translated into an expressive strategy on another.
Figure 6 showed that different grace notes scale differently over tempo than others. In particular, grace notes 2, 7, 8, 9 and 10 scale significantly more than would be expected if grace note timing were relationally invariant. There is no single music-theoretical category into which these grace notes fall. It is therefore difficult to make any definitive statement regarding why this effect should occur, but it does seem that longer grace notes scale more over tempo than shorter ones. Whether this is due to some general timing principle, such that longer intervals simply tend to scale more with tempo, is impossible to ascertain from this study alone. What is more certain is that for this highly skilled pianist, consistent deviations for proportional duration may be observed and we would argue that this is strong evidence against relational invariance in musical timing. These results are in contrast to Repp’s (1994) finding that grace notes were relationally invariant over tempo, although this should not be interpreted too strongly as the grace notes in his study were, as he himself admits, rather unusual examples. Our results do not replicate the findings of Desain and Honing (1994). They found that, although grace notes 4 and 5 occur in very similar situations, they were treated in a radically different way: grace note 4 got slightly longer as the tempo got lower, whereas grace note 5 got shorter as the tempo got lower. Similarly, although grace notes 3 and 11 are virtually identical, they found a significant difference between the two. Desain and Honing do remark that more data were needed to come to a precise description and explanation of these different behaviors of the grace notes. We found no evidence that our pianist treated grace notes 4 and 5, or grace notes 3 and 11 in a different way.
Although we cannot say anything about the absolute placement of the grace notes we can make some definitive statements about their relative placement. Figure 7 shows that all the grace notes consistently occur before the reference point (the left-hand note) and that the main note occurs some 12 ms before the reference point. This last phenomenon can be explained by the fact that the main note is the melody note and therefore leads the accompaniment (Palmer, 1989). The grace note occurs earlier and earlier when the tempo gets lower and does not push the main note back relative to the accompaniment note as it gets longer. Such a pattern of timing does not fit in with the two types of ornament identified by Desain and Honing (1994): appogiature or acciaccature. Both these types of ornament are normally assumed to be played such that they occur at the same time as the other onsets of the harmonic context (in this case the left-hand onset). In the case of appogiature, the following note is delayed significantly. One might expect to find evidence of the appogiature in an increasing asynchrony between left and right hand, with the right hand occurring later than the left. This is not what is found in our study. Neither does our study give evidence for the grace note being an accaciatura. In the case of the accaciature the grace note and the following note are played simultaneously, with the grace note being released quite quickly. (see Neumann, 1986:42) However, leaving aside the precise musicological distinctions between these types of ornament, it is clear that the pianist is making a distinction between long and short grace notes, and playing them such that they take time from the preceding note. This actually makes considerable musical sense. When the grace note takes time from the preceding note, instead of the following note, the regular rhythm of triplets and the irregular rhythm of quarter note plus eighth note of the melody are maintained. If the grace note is played in the time of the main note, it distorts the regular rhythm of triplets, by making the rhythm irregular and it distorts the 2 to 1 ratio of the irregular rhythm, by making it regular (1:1:1) or unidentifiable. Another explanation is that grace notes might be played as if their duration comes from the preceding note where they are considered more strongly attached to this note than to the subsequent note. All the grace notes in this piece apart from grace note 6 either elaborate the harmony of the previous note, or simply repeat the same pitch. Grace note 6 however, is an unprepared suspension, a tone above the following melody note. This grace note takes up an interval of less than 20% of an eighth note: it has the shortest mean proportional IOI of all the grace notes. It takes time from the previous note, since the mean asynchrony between main right hand note and left hand remains negative across the 45 repetitions of grace note 6. A possible explanation for the timing of this grace note is that the performer was actively avoiding accentuating the dissonance between grace note 6 and the left hand note, by playing the grace note before the left hand onset and keeping its IOI relatively short. One might further speculate that this was in line with the pianist's explicit attention to the sung character of the melody:
"I also thought about how to play the grace notes: that’s a difficult matter. There are of course official rules for this, but I thought: if I were a singer, how would I do it? It’s important where you place the grace note [plays the 2nd grace note in different ways]. Based on my intuition, hoping that’s correct, I decided to play them just before, so the listener has time to experience the interval downwards. If I would play it on the beat it would be stressed too much… With the authentic performance practice, there are of course a lot of rules about everything, but with a songlike theme like this one, you can be freer. Of course, you have to pay attention to what sounds comfortable."
Conclusions
In this study, although our findings are confined to the study of one expert performer’s performances of a single piece, we believe a number of firm conclusions may be drawn regarding the timing of grace notes. The most important of these is that although musical structure may have an important influence upon their execution, such structural constraints cannot alone explain the differences we find in the relative length of grace notes, and do not seem to play a role in the changes in their execution at different tempi. Instead, the major influence on grace note timing seems to be more stylistic. The "character" of the melody, its origin in an operatic aria, combines with local differences in interval structure, small and large melodic leaps, resulting in subtle interpretative decisions that influence the length allotted to each grace note.
In addition, this study considerably weakens the notion that grace note timing can be explained by any theory that predicts relational invariance across a range of tempi. Although we cannot propose any substantive theory to explain why certain grace notes in this study were relationally invariant, and others not, it seems unlikely to us that this result could be explained by motoric constraints alone. Although it remains unclear what factors may play a role in changing the relative lengths of grace notes at different tempi, it is clear that subtle stylistic factors might again have played a role. As the pianist noted:
"You can always make a tempo sensible. But the tempo shouldn’t make the piece too jumpy, nor too dreamy and romantic. I would look for something songlike and simple."
References
Clarke, E. F. (1985). Structure and expression in rhythmic performance. In P. Howell, I. Cross, and R. West, (Eds.), Musical structure and cognition. London: Academic Press. Clarke, E. F. (1995). Expression in performance: generativity, perception and semiosis. In J. Rink (ed.), The Practice of Performance: Studies in Musical Interpretation. Cambridge: CUP.
Desain, P. and Honing, H. (1993). Tempo curves considered harmful. In J. D. Kramer (ed.), Time in Contemporary Musical Thought, Contemporary Music Review, 7 (2), 123-138.
Desain, P. and Honing, H. (1994). Does expressive timing in music performance scale proportionally with tempo? Psychological Research, 56, 285-292.
Desain, P., Honing, H. and Heijink, H. (1997). Robust Score-Performance Matching: Taking Advantage of Structural Information. In Proceedings of the 1997 International Computer Music Conference. San Francisco: International Computer Music Association, 337-340.
Donington , R. (1963). The interpretation of early music. New rev. ed. London: Faber and Faber, 1989, 189-214, 222-235, 620-640.
Feldman, J., Epstein, D. and Richards, W. (1992). Force dynamics of tempo change in music. Music Perception, 10, 185-204.
Gabrielsson, A. (1987). Once again: the theme from Mozart's Piano Sonata in A major: A comparison of five performances. In A. Gabrielsson (Ed.), Action and Perception in Rhythm and Music. Stockholm: Royal Swedish Academy of Music.
Gentner, D. R. (1987). Timing of Skilled Motor Performance: Tests of the Proportional Duration Model. Psychological Review, 94 (2), 255-276.
Kronman U. and Sundberg, A. (1987). Is the musical ritard an allusion to physical motion? In A. Gabrielsson (Ed.), Action and Perception in Rhythm and Music. Stockholm: Royal Swedish Academy of Music.
Longuet-Higgins, H. C. and Lisle, E. R. (1989). Modelling music cognition. Contemporary Music Review, 3, 15-27.
Mackenzie, C. L. and Van Eerd, D. L. (1990). Rhythmic Precision in the Performance of Piano Scales. Motor Psychophysics and Motor Programming. In M. Jeannerod (ed.), Attention and Performance: Motor Representation and Control, 13, 375-408. NJ: Hillsdale.
MIDI Manufacturers Association (1996). The Complete MIDI 1.0 Detailed Specification Version 96.1. La Habra: MIDI Manufacturers Association.
Neumann, F (1978). Ornamentation in Baroque and post-Baroque music: with special emphasis on J. S. Bach. Princeton & Oxford: Princeton University Press.
Neumann, F. (1986). Ornamentation and Improvisation in Mozart. Princeton & Oxford: Princeton University Press.
Palmer, C. (1989) Mapping Musical thought to musical performance. Journal of Experimental Psychology: Human Perception and Performance, 15 (12), 331-346.
Palmer, C. (1996). On the Assignment of Structure in Music Performance. Music Perception, 14 (1), 23-56.
Palmer, C. (1997). Music Performance, Annual Review of Psychology, 48, 115-138.
Repp, B. H. (1990). Patterns of expressive timing in performances of a Beethoven minuet by 19 famous pianists. Journal of the Acoustical Society of America, 88, 622-641.
Repp, B. H. (1992). Diversity and commonality in music performance - an analysis of timing microstructure in Schumann’s Traumerei. Journal of the Acoustical Society of America, 92 (5), 2546-2568.
Repp, B. H. (1994). Relational invariance of expressive microstructure across global tempo changes in music performance: An exploratory study. Psychological Research, 56, 269-284.
Repp, B. H. (1995). Quantitative Effects of Global Tempo on Expressive Timing in Music Performance: Some Perceptual Evidence. Music Perception, 13 (1), 39-57.
Rink, J. (ed.)(1995). The Practice of Performance: Studies in Musical Interpretation. Cambridge: CUP.
Shaffer, L. H. and Todd, N. P. (1987). The interpretive component in musical performance. In A. Gabrielsson (ed.), Action and Perception in Rhythm and Music. Stockholm: Royal Swedish Academy of Music.
Sloboda, J. A. (1983). The communication of musical metre in piano performance. Quarterly Journal of Experimental Psychology, 35A, 377-396.
Todd, N. P. (1985). A model of expressive timing in tonal music. Music Perception, 3, 33-58.
Todd, N. P. (1989). A computational model of tempo. Contemporary Music Review, 3, 69-88.
Todd, N. P. (1992). The dynamics of dynamics: A model of musical expression. Journal of the Acoustical Society of America, 91, 3540-3550.
Todd, N. P. (McA.) (1995). The kinematics of musical expression. Journal of the Acoustical Society of America, 97, 1940-1949.
Acknowledgements
This work was undertaken as part of the ‘Music, Mind Machine’ project at the Nijmegen Institute for Cognition and Information (NICI) which is funded through a Pionier grant from the Netherlands Organization for Scientific Research. The authors would like to express thanks to Heike Martensen (Mathematical Psychology, NICI) for her assistance with some of the statistical issues in this study. Especial thanks are due to Bart van de Roer, for his patience, his articulate responses to our questions, and his excellent playing.
Appendix 1
