From Time to Time:
The Representation of Timing and Tempo
Henkjan Honing
MMM Group, NICI, University of Nijmegen,
P.O. Box 9104, 6500 HE Nijmegen, The Netherlands
Music Department, University of Amsterdam,
Spuistraat 134, 1012 VB Amsterdam, The Netherlands.
honing@nici.kun.nl
To be published as:
Honing, H. (2001) From Time to Time: The Representation of Timing and Tempo. Computer Music Journal. Vol. 25(3). Fall 2001 (see www.nici.kun.nl/mmm/abstracts/mmm-1.html).
Keywords
Knowledge representation, music cognition, music performance, computational modeling, musical time.
Abstract
The first half of this paper reviews existing representations of timing and tempo as used in computational models of music cognition and in programming languages for music. They are presented in a formal way, their differences are discussed and some refinements are proposed. The second half of the paper introduces an alternative representation and model for time transformation, named timing functions, that differs in two aspects from earlier proposals. First, timing is seen as a combination of a tempo component (expressing the change of rate over a fragment of music), and a timing (or time-shift) component that describes how events are timed (e.g., early or late) with respect to this tempo description. Second, timing can be specified in relation to the temporal structure (e.g., position in the phrase or bar) and global tempo.
[this page is not part of the published paper]
Timing plays an important role in the performance and appreciation of almost all types of music. It has been studied extensively in music perception and music performance research (see Palmer 1997 for a review). The most important outcome of this research is that a large part of the timing patterns found in music performance –commonly referred to as expressive timing– can be explained in terms of the musical structure, like the recurrent patterns associated with the metrical structure that are used in jazz swing or the typical slowing down at the end of phrases in classical music from the Romantic period. These timing patterns help in communicating the temporal structure (such as rhythm, meter, or phrase structure) to the listener. Furthermore, timing is adapted with regard to the global tempo: at different tempi other structural levels of the music are emphasized and the expressive timing is adapted accordingly. In short, in music performance there is a close relationship between expressive timing, global tempo (or rate) and temporal structure – one cannot be modeled without the other (see Figure 1).
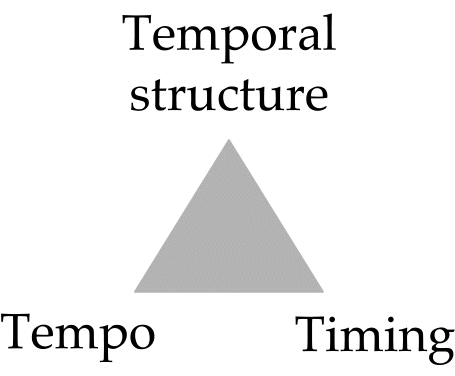
Figure 1. Three aspects of music performance that are closely related: expressive timing, global tempo (or rate) and temporal structure (such as rhythm, meter or phrase structure).
Existing computational models of expressive timing (see Clarke 1999; Gabrielsson 1999) are mainly concerned with explaining tempo variations, using tempo curves (specifying tempo or 1/duration as a function of the position in the score) as the underlying representation. Although a useful way of measuring tempo patterns in a performance, tempo curves were shown to fall short as an underlying representation of timing, from a musical perspective (Desain and Honing 1991; 1993) and a psychological perspective (Desain and Honing 1994). For instance, some types of timing, like chord spread (the asynchrony in performing a chord), ornaments (like grace notes), or the timing between parallel voices simply cannot be measured or represented as tempo deviations. Furthermore, in some musical situations or styles of music, where the global tempo is mostly constant, event-shift (Bilmes 1993) – measured as the deviations with respect to a fixed beat or pulse in a constant tempo –, seems a more natural way of representing timing.
This paper will, first, review existing representations of timing and tempo common in computational models of music cognition and in programming languages for music. Their differences are discussed and some refinements will be proposed (referred to as time-maps or TMs). The second part presents an alternative representation and model for time transformation, so-called timing functions (TIFs; an acronym chosen to distinguish them from time functions [TFs, i.e. control functions]; Desain and Honing 1992). This knowledge representation differs in two important aspects from earlier proposals. First, expressive timing is seen as a combination of a tempo component (expressing the change of rate over a fragment of music), and a timing (or time-shift) component that describes how events are timed (e.g., early or late) with respect to this tempo description. Second, expressive timing can be specified in relation to the temporal structure (e.g., position in the phrase or bar), as well as in terms of performance-time, score-time and global tempo. In addition, timing functions (TIFs) support compositionality (how simple descriptions can be combined into more complex ones) and maintain consistency over musical transformations (how these descriptions of timing and tempo should adapt when other parts of the representation change), both important design criteria of the formalism.
Another design criterion is that timing transformations (e.g., the application of an expressive timing model to a score representation) are part of the representation, instead of only acting on a score – the difference between a knowledge representation and a data representation. In order to realize this, it is crucial to have access to the timing transformations themselves – not only to the result of their application (as is the case in most music representation systems [See, e.g., Dannenberg 1993]). Or, in other words, to be able to do transformation after transformation (as needed in music sequencers and expression editors), or compose a number of transformations into one more complex transformation (essential in programming languages for music or in combining partial computational models of expressive timing), the transformations themselves should be an object in the representation, not just functions applied to it. A practical example will clarify this.
Imagine the situation of an editor for expressive timing where you just applied a jazz-swing transformation to a score representation, resulting in a performance with some expressive timing added. Next, you apply a global tempo transformation to this result, simply speeding up the performance. The result of this second transformation, however, will sound strange. This is because the swing pattern is closely related to the beat at the original tempo, which is now changed by the tempo transformation. In order to obtain the desired result, the swing pattern transformation has to adapt itself, in retrospect, to the new tempo. It has, in fact, to be a function of tempo not known at the time of application. In general, this means that previously applied transformations (or nested transformations, for that matter) sometimes have to adapt themselves when new transformations are applied. (Note: an alternative could be to describe, with every new transformation, how all the other aspects of the representation should be kept consistent. However, this is a virtually impossible task.) Defining this so-called “behavior under transformation” is essential in situations where a representation of timing is actually used (such as in music editors or computational modeling), instead of being a static description of a performance – the difference between a knowledge representation and a data representation (cf. “The Vibrato Problem”; Honing 1995; Dannenberg, Desain and Honing 1997).
The Representation of Tempo and Timing
There are a number of ways of representing expressive timing. The three most encountered ones will be described here. Tempo functions are mostly used in music psychology research. They form the output of several generative models of expressive timing (e.g., Clynes 1995; Todd 1992; Sundberg 1988). Most of this research is concerned with piano music from the Baroque and Romantic period, where indeed tempo rubato (expressive tempo fluctuations), is the most evident type of expressive means. In some, more recent studies, time-shift (or event-shift) patterns, i.e. timing measured as deviations from a regular pulse, are analyzed. For example, in the study of timing in jazz ballads (Ashley 1996) or in Cuban percussion music (Bilmes 1993). In computer music time-maps are mostly used (also referred to as time-deformations [Anderson and Kuivila 1990] or time-warps [Dannenberg 1997]). They express performance-time directly as a function of score-time, and can, in principle, describe both time-shift and tempo-change.
Mathematically, tempo changes can be expressed as time-shifts and vice versa (see Figure 2): they are equivalent (under some constraints that will be mentioned later). However, they are musically very different notions. Tempo change is associated with, for example, rubato, accelerando (speeding up) and decelerando (slowing down), while time-shift has to do with, for instance, accentuating notes by delaying them a bit or playing notes “behind the beat,” both apparently independent of the tempo. Also, from a perceptual point of view, it seems that listeners do perceive tempo relatively independent from timing (see Related Work).
Before proposing a formalism that is in line with these observations, the three existing representations mentioned above (i.e. tempo curves, time-shift functions and time-maps; see Figure 2) will be presented. Next to their formal definition (in a functional style, without any typing for simplicity), their composition (in the mathematical sense) will be shown, compositionality being an essential strength of all three alternatives.
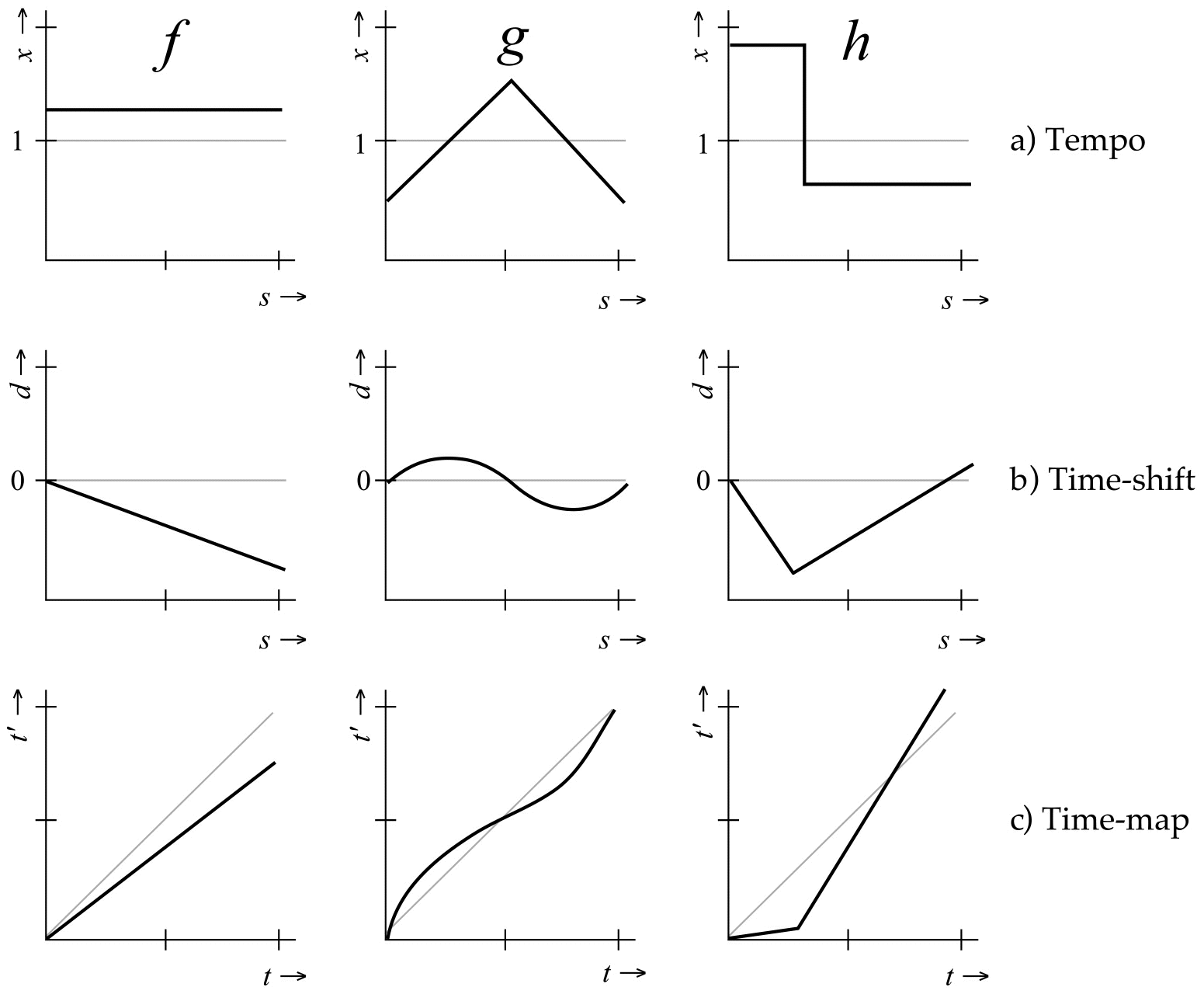
Figure 2.
Three arbitrary tempo functions, 
,
,
and 
(a), and their equivalent representations as time-shift function (b)
and time-map (c). 
depicts
a constant tempo, 
a
linear tempo-change (a “give and take” rubato; see Figure
3 for an example in musical notation), and 
a sudden tempo-change. For a restricted class of functions (to which 
,
,
and 
belong) one can freely convert from one representation to the other
(see text for details).
A tempo function (or tempo curve) can be expressed as a function of score-time (s, a rational number denoting symbolic score-time) returning a tempo factor (x, a real number):
(1)
To obtain the performance-time at score-time s, one has to integrate the tempo function until that score-time. Tempo functions can be composed by multiplying their individual results, or formally:
(2)
Which states that the composition (
)
of two tempo functions (
and
)
applied to a score-time (s), is defined as applying
each individual tempo function to that score-time and multiplying (
)
the results.
A time-shift function (or event shift) can be expressed as a function of score-time (s, a rational number denoting symbolic score-time) returning a deviation interval (d, a real number), i.e. the amount of time an event is shifted with respect to its score-time:
(3)
To obtain a performance-time at score-time s, one can simply add the deviation d to it. In principle, time-shift functions can change the order of events with respect to the score. (Note that, when this occurs, a time-shift function cannot be converted into a tempo function anymore.) Time-shift functions can be composed by adding the results of the components:
(4)
Finally, a time-map is defined as a function from pre-perturbed time (t, a real number) to perturbed time or performance-time (t', a real number):
(5)
They can be composed using function composition:
(6)
Time-maps can take score-time (s) as argument, but this is then just a special case of pre-perturbed time. This has, as will be shown in the next section, its implications for composing time-maps.
Figure 2 shows some examples of prototypical
shapes of tempo functions, and their representation as time-shift
function and time-map: a constant tempo (
),
a gradual tempo change (
),
and an instantaneous tempo change (
).
As an illustration in common music notation the application of
function 
(a simplistic “give and take” rubato ) is shown in Figure
3.
Figure 3.
A time-map (a), a score (c), and a performance (b) with spacing
indicating its timing. The time-map represents a “give and take”
rubato with an acceleration (from t1
to t2)
and a deccelaration (from t2
to t3),
but with regularly timed beats (at t1,
t2, and t3) (see tempo
function 
in Figure 2). The result of applying the time-map (a) to the score
(c) is shown in (b). Solid gray lines indicate the regularly timed
beats and the dashed gray line marks an example of a delayed
note.
Time-maps are defined as continuous, monotonically increasing functions (Jaffe 1985). Which means that time is not allowed to reverse or jump ahead to allow conversions from time-maps to tempo-functions and time-shift functions and vice versa (The functions shown in Figure 2 belong to this class).
The composition of two time-maps can be visualized
as shown in Figure 4. In there, time-map 
is rotated 90 degrees to the left to
connect its x-axis (input) to the y-axis (output) of time-map 
,
depicting the composite time-map 
(or 
).
Please note that 
and 
are used throughout this paper to represent both basic and complex,
composed time-maps.
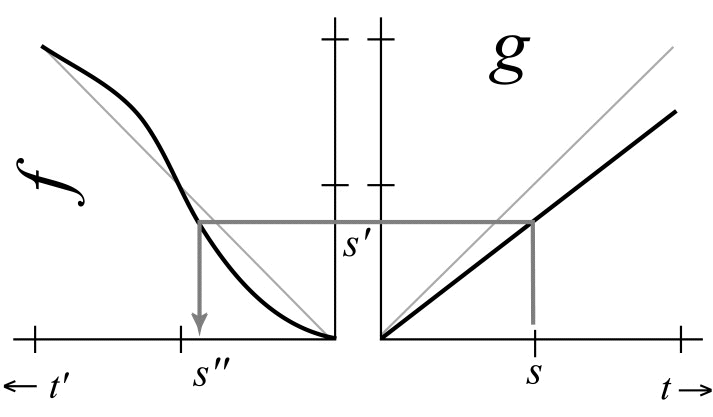
Figure 4.
Composition of two time-maps (
):
Time-map 
is
rotated 90 degrees to the left to connect its x-axis (input) to the
y-axis (output) of time-map 
.
The gray arrow marks how score-time s is mapped to a
perturbated-time s' by 
,
and, successively, how this s' is mapped to s" by 
.
It is the simplicity of composition and the direct availability of performance-time (by simply looking it up in the time-map, instead of, e.g., the need for integration in tempo functions) that makes the time-map the representation of choice in most computer music systems. However, time-maps have some limitations that have to be resolved before they can be used as a flexible basis for a representation of timing.
Restrictions to the Time-Map Representation
Below some of the restrictions to time-maps will be discussed, followed by an extension that resolves some of these (referred to as extended time-maps or TMs).
Score-time is Lost in Composition
One of the problems with time-maps (compared
to time-shift and tempo functions) is that score-time is lost in
composition (see Eq. 6). For example, in Figure 4, 
is accessed with s' instead of s (the transformed instead of the original
score-time). This is problematic when timing needs to be expressed in
terms of score position, such as swing, or other types of timing
related to metrical time (i.e. patterns linked to the metrical or
phrase structure). However, this can simply be solved by making a
time-map a function of both types of musical time: performance-time
and score-time (this will explained below). Note again that 
or 
can be complex, composed time-maps, so simply reversing the order of
application does not solve the problem.
There are numerous ways of concatenating two arbitrary time-maps. However, from a musical perspective two alternatives come to mind: joining them in performance-time (see Figure 5a) or in score-time (see Figure 5b). The first can be interpreted as a continuing change of tempo, the latter as shift of time, changing the timing of events without altering the baseline tempo. The first type of concatenation is what is supported in Anderson and Kuivila (1990) and Dannenberg (1997). The second type of concatenation is illegal in all time-map implementations, since the resulting time-map is not monotonously increasing: time-shift functions can change the score order of notes. However, from a musical perspective this is a perfectly plausible. For example, while for a sequence of notes the tempo is constant or gradually changing, some notes can be accented by performing them somewhat early or late.
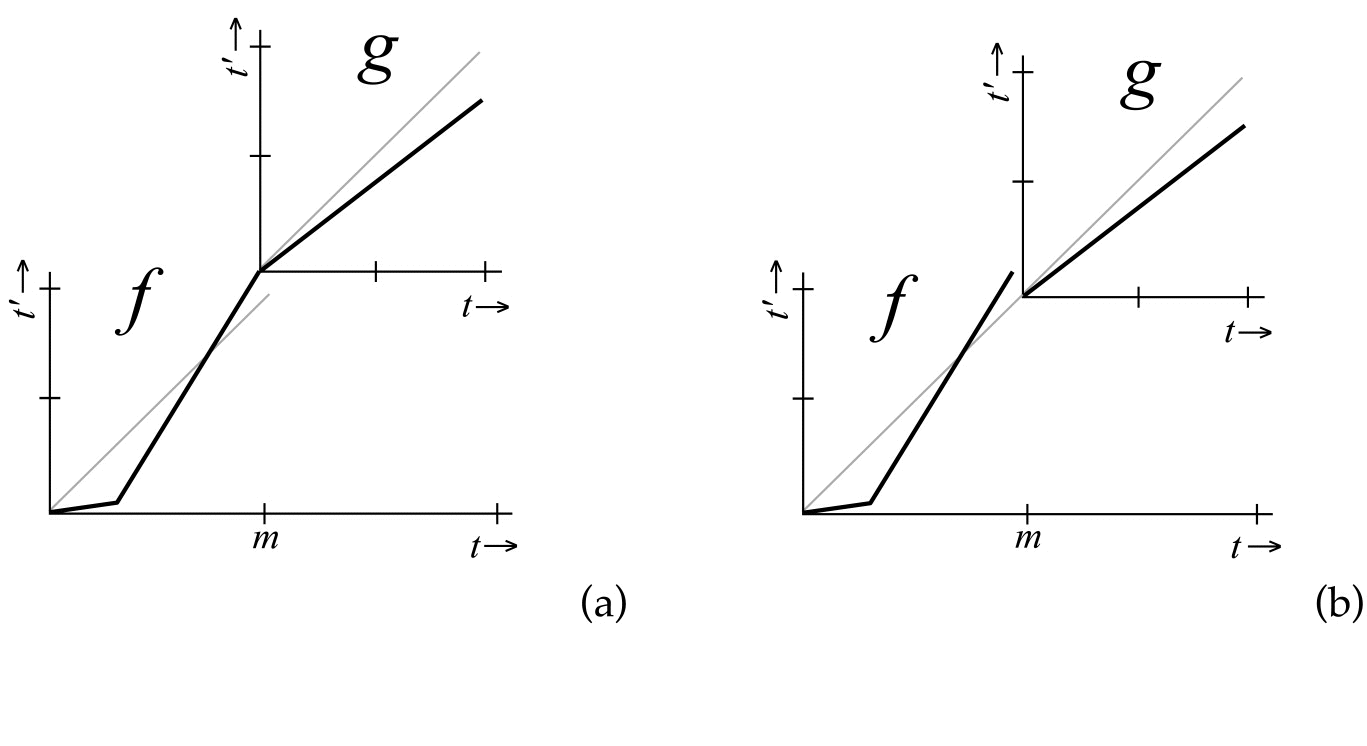
Figure 5.
Two ways of concatenating 
and 
in score-time point m: joining them in
performance-time (a) or score-time (b).
But even with the realization for the need for different kinds of concatenation, one has to choose one or the other type, since we cannot tell, from the time-map itself, whether is the result of a tempo-change definition or an interpretation as time-shift. This suggests that one needs to keep both types of timing (tempo-change and time-shift) separate and concatenate each in its own typical way (see under Timing Functions).
Access to Score and Performance Duration in Composition
Besides the need for score-time in the
composition of time-maps (as discussed above), even more temporal
information is necessary to make the composition of time-maps as
simple as possible. This can be illustrated by looking in detail at
the composition of the two time-maps shown in Figure 6. Let’s
interpret 
(Figure 6a) as a simplistic “give and take” type of
rubato (see also musical example in Figure 3) synchronous at every
beat (score-times b, s
and e) speeding up and
slowing down between them, and 
(Figure 6b) as a faster constant tempo. In combining these two
time-maps, one expects to get a composite time-map with a faster
tempo and a timing pattern that slows down and speeds up again, but
synchronizes on every beat (i.e. the two beats have the same length: 
).
However, as can be seen in Figure 6c, the score-time s
is mapped to performance-time s' by 
and accesses 
in the wrong position (i.e. not in s,
but some time before it), resulting in beats of unequal length (
).
What is needed is a way of linking a time-map to a
temporal interval (e.g., the length of a bar). As such, a time-map
can adapt its definition according to the actual length (in
performance time) of the interval, i.e. the length as a result of all
previously applied time-maps (in this example 
).
As an example, in Figure 6d 
is adapted to fit the current length of the bar in performance-time
(by inspecting the result of applying 
),
resulting in a correct lookup in 
.
(Here, again, changing the application order is not a solution, since
and 
can be complex, composed time-maps).
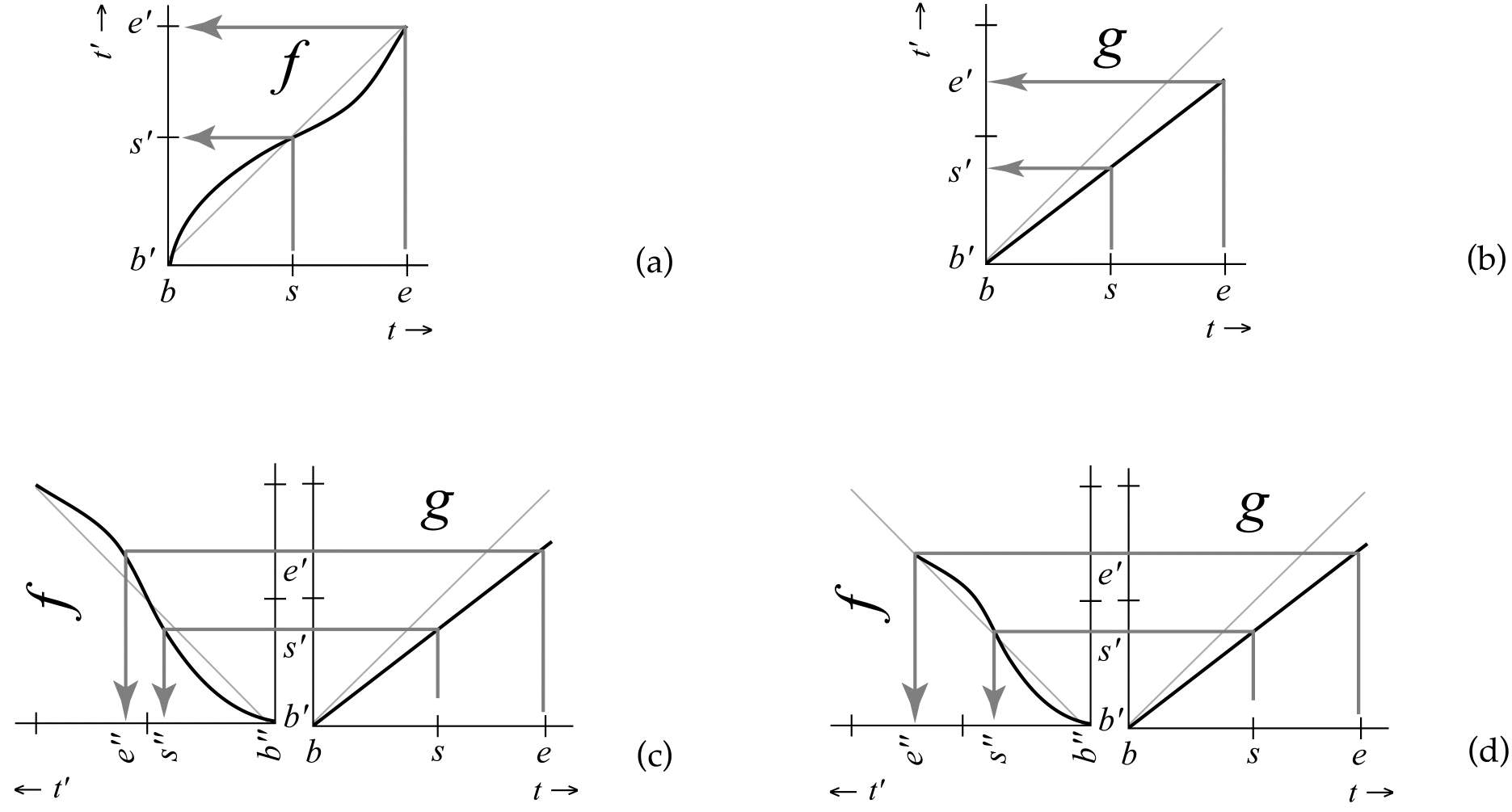
Figure 6.
Problem in the composition of time-maps: a time-map describing a
simple “give and take” type of rubato that
is synchronous at the every beat (score-times b,
s and e)
(a), a time-map of a faster constant tempo (b), an erroneous
composition of two time-maps (
is accessed in the wrong position) (c), and a correct composition,
because 
is adapted to fit the current length of the bar in performance-time
(d); Both beats (from b' to s' and from s'
to e') stay of equal
length, through at a faster global tempo. (Note that 
and 
can be complex, composed time-maps, so simply changing the order of
composition is not a solution).
The problem of losing score-time in composition and explicit support of two types of concatenation will be resolved in an extension of time-maps (TMs). The third problem of relating a time-map to a temporal interval will be resolved by distinguishing between two types of time-maps (in timing functions [TIFs]) and relating them to a temporal interval in generalized timing functions (GTIFs).
To resolve the restrictions on time-maps
discussed above, two types of time-maps (indicated in plain font)
will be defined, one representing time-shift (
) and one representing tempo-change
(
).
Both are functions of performance-time and score-time, and return a
perturbed performance-time t'.
(7)
(8)
Both can be composed in the same way (Note: 
and
without superscript are used when the type is irrelevant for an
operation):
(9)
Depending of the type of time-map at hand one can
decide for the type of concatenation. 
denotes the concatenation function, with m
indicating the score-time at
which the two functions will be joined. The first, as required for
time-shift time-maps (cf. Figure 5b):
(10)
Which states that the concatenation (
)
of the time-maps 
and 
applied to a score-time (s) is the application of 
before score-time m, and application of 
after that point. (Note: the issue of over which temporal interval
these functions are defined will be addressed later).
The second type of concatenation is required for tempo-change time-maps (cf. Figure 5a):
(11)
In here, the function Dm calculates a
new time-map function, shifted in time such that 
connects to where 
ended:
(12)
What is calculated here is simply the difference
(i.e. the difference in height between the tempo baselines [gray
lines] shown in Figure 5a) between score-time m
and its corresponding performance-time m'
(the result of applying the function 
to score-time m and
untransformed performance-time, also m),
added to the successive tempo-change function 
.
Having introduced two types of time-maps and their respective definition for composition and concatenation, I will continue with the description of timing functions that will integrate the two types of time-maps.
The two aspects of timing, describe above,
will be combined in one timing function
(TIF): a tuple consisting of a time-shift function (
)
and a tempo-change function (
).
The symbols f and g
(boldface) are used to refer to such timing functions:
(13)
Or, in computational terms, a TIF is a data
structure containing two time-maps, one describing time-shift and the
other tempo-change. These will stay separate in composition and/or
concatenation, since this is different for each type of timing. Only
in the end, when actually applying a TIF, the components are
combined: first applying the tempo-change component (
)
and then the time-shift component (
)
to the current performance-time and score-time.
The evaluation function E describes how (given a TIF, a score-time, and a performance-time) the result (a new performance-time) is obtained:
(14)
This evaluation order makes sure that first the tempo baseline is obtained from which the time-shift descriptions deviate. The order in which individual components are combined is not relevant anymore. (Note: One could however, in cases where one wants to have explicit control over this application order, add a third function to the tuple that determines this order: a function of, respectively, the two TMs, s and t).
The composition of TIFs is straight forward. It simply is the composition of the individual components:
(15)
Which states that the composition of the timing
functions f and g,
is defined as the composition of their time-shift components (
and 
)
and their tempo change components (
and
).
Both are composed as defined in Eq. 9.
Concatenation of time-maps can now be described correctly by concatenating the time-shift component in a different way than the tempo-change component. Concatenation of two TIFs is defined as (with m indicating the score-time at which the two functions will be joined):
(16)
With the time-shift components (
and 
)
being concatenated according to Eq. 10, and the tempo-change
components (
and
)
according to Eq. 11.
Generalized Timing Functions (GTIFs)
Finally, I will discuss a generalization of timing functions that allows them to be related to the temporal structure (instead of only the current score-time and performance-time). To be more specific, generalized timing functions (GTIFs) will have access to the duration of the interval it is applied to (e.g. a bar or a phrase), its current position (in both score-time and performance-time), and the current tempo. The key idea in realizing this is to provide the definition of a timing function with access to the begin-time and end-time of a temporal interval (in score-time) over which the function is defined, together with the complete “underlying” time-map: the composite function of all previously applied timing transformations. A GTIF is, in fact, a timing function constructor (indicated in italic boldface):
(17)
Which states that the constructor 
is a function of b
(begin-time, a rational number denoting symbolic score-time), e
(end-time, a rational number denoting symbolic score-time), and 
(a TIF of all previous applied timing transformations). It returns a
new TIF 
that has access to all relevant temporal information (both
score-times and performance-times) of that time interval.
Composition of two GTIFs is defined as:
(18)
Concatenation of two GTIFs at time point m (a rational number denoting the point where the two functions are joint in metrical time), is defined as the concatenation of two TIFs attached to interval <b, m] and <m, e] respectively:
(19)
To give an idea of how one could implement GTIFs in a general programming language, some aspects of a realization in Common Lisp (Steele 1990) are presented below.
An implementation of timing functions will consist of a number of constructs to define (e.g., make-tif), compose (e.g., compose-tif), concatenate (e.g., concatenate-tif) and evaluate (e.g., tif-funcall) the different types of timing functions (i.e. TMs, TIFs, and GTIFs). A complete implementation cannot be presented here, but I will give an example of a GTIF definition to illustrate the actual communication of timing information. (A micro-version implementation of timing functions will be made available as an extension to GTF [Desain and Honing 1992; Honing 1995] at https://www.nici.kun.nl/mmm).
Figure 7 shows an example in Common Lisp of a timing function definition. It shows the constructor functions make-tif (Eq. 13), anonymous-gtif (Eq. 17) and anonymous-tm (Eq. 7) (The latter two being equivalent to lambda abstraction), as well as the evaluation function tif-funcall (Eq. 14). In the part named <body> the actual definition (e.g., a model describing how timing is dependent on global tempo and its metrical position) can be placed. These functions (TIFs) can be directly expressed in terms of score-time (begin, end, and/or duration) and performance-time (begin, end, and/or duration) of the temporal interval over which the they are defined.
Having this information available, for example, a
time-map describing how a jazzy groove pattern is related to the
metrical structure and the current tempo, can expressed by the
time-shift component of a GTIF. It will have access to all previously
applied tempo transformations (i.e. the tempo component of 
)
and can adapt accordingly. As another example, models of expressive
tempo change that are stated in terms of metrical position (e.g.,
Clynes 1995) or position in the phrase structure (e.g., Todd 1992)
can be expressed in the tempo-change component of a GTIF. While most
these expressive timing models do not state how they should change
with, e.g., global tempo, the formalism in principle allows for this
and can support the way these partial models can be combined.
Figure 7. Code example (in Common Lisp) of a timing function definition (see text for details).
Below I will summarize related work on the representation of timing and tempo in both the computer music and music cognition research communities.
The representation of musical time has been a topic of numerous proposals in music representation research (see Roads 1996; Dannenberg 1993; Honing 1993) and a number of formalisms have been proposed. Rogers, Rockstroh and Batstone (1980) introduce a way to express tempo changes as a function of beat position (score-time) to real-time (performance-time). Jaffe (1985) presented similar ideas and promotes the use of a time-map (as an alternative to tempo functions). Anderson and Kuivila (1990) introduce tempo functions that can be concatenated, named time-deformations. However, their tempo functions and time-shift functions (named pause) are not integrated in one representation, score-time is lost in composition (like time-maps), and behavior under transformation is not supported. Dannenberg (1997) proposes a generalization of his earlier work on the Nyquist system for sound synthesis and composition. This research stresses the importance of behavior under transformation (referred to as “behavioral abstraction”) and proposes an integrated representation for discrete events and continuous signals named time-warping. It supports time-shift and tempo transformations (named shift and stretch). However, the relation between time-warps and temporal structure (e.g., to give time-warps access to duration) can not be made because of intrinsic design decisions in Nyquist (duration is not available because of its causal, real-time design; see Honing 1995).
Next to the formalization of timing and tempo, various computer music systems have been proposed that attempt to model these phenomena (see, e.g., Scheirer 1998; Cemgil, Kappen, Desain and Honing 2001). Most of these systems use either tempo-curves, time-shift functions, or time-maps as their underlying representation.
Music Cognition
The representation of time is also an important issue in music perception and cognition research. In the cognitive sciences several proposals have been made, especially in the domain of temporal logic (Benthem 1991), to be able to reason about events occurring in time, resulting in proposals that promote the representation of time as intervals (Allen and Ferguson 1994) or as points (McDermott 1982; see Marsden 2000 for an overview of applying temporal logic to music). These proposals are all essentially discrete. In music representation research, however, symbolic and numerical descriptions in both the discrete and continuous domain are needed (like discrete notes and their rhythmic structure, contrasted with continuous descriptions of , e.g., timing), which have to be integrated in one representation (see Dannenberg, Desain and Honing 1997).
Also in music perception a distinction is made between the discrete rhythmic durations, as symbolized by the note values in a score, and the continuous timing variations that characterize an expressive performance (Clarke 1999). A listener is able to separate the temporal information of, for example, an expressively performed rhythm into note durations, expressive timing, and tempo information.
The knowledge representation proposed in this paper makes these three aspects explicit by introducing a way in which timing can be expressed in terms of the temporal structure and global tempo (see Figure 1). Secondly, this representation differentiates between two components of musical time: tempo, the perception of change of rate related to a process called beat-induction (see Desain and Honing 1999), and timing, the perception of the minute time deviations related to categorical rhythm perception (see Clarke 1999).
While in the music performance literature there is quite some discussion on the specific shape of, especially, the tempo functions and their relation to human motion (see Todd 1999; Friberg and Sundberg 1999; Desain and Honing 1996), the proposed formalism does not make any restrictions as to their specific shape: these models can all be represented in the tempo component of a timing function. Yet, the representation stresses the importance of types of timing that are relatively independent of tempo change, and it allows for a description of how these types of timing interact. For example, how “laid-back” timing in a Jazz fragment (expressed in the time-shift component of a timing function) should adapt itself to the current global tempo (expressed in the tempo-change component of a timing function).
However, it should be noted that it is still unclear whether the perception of tempo and timing are two separate perceptual processes or one and the same, and what the precise cognitive constraints on the perception of timing are (e.g., Repp 1992). There is a continuing effort to try and understand what precisely constitutes tempo, how timing is dependent of global tempo or absolute rate, and how it is perceived and performed (Palmer 1997; Gabrielsson 1999), as well as a discussion on how to computationally model these phenomena (see Desain, Honing, van Thienen and Windsor 1998).
The first half of this paper reviewed existing representations of timing and tempo common in computational models of music cognition and in programming languages for music. A formal analysis revealed their differences and some refinements were proposed. The second half of the paper introduced a knowledge representation of musical time that differs in two important aspects from earlier proposals. First, timing is seen as a combination of a tempo component (expressing the change of rate over a fragment of music, such as tempo rubato), and a timing (or time-shift) component that describes how events are timed (e.g., early or late) with respect to this tempo description. Second, timing can be specified in relation to the temporal structure (e.g., position in the phrase or bar), as well as performance-time, score-time, and global tempo.
However, the proposed representation covers only a part of the timing phenomena observed in music performance, concentrating on a continuous description of onset-timing. For instance, asynchrony, like chord spread, is not explicitly supported (functions that map one score-time to different performance times), neither is articulation (offset timing and its relation to musical streams and structure). These are relatively complex aspects of timing that are still little understood. These will be topic of further research and future extensions.
Special thanks to Peter Desain for, as always, inspiring discussions and substantial help in the design of timing functions. Roger Dannenberg is thanked for many stimulating discussions on this and related work. Renee Timmers commented on an earlier version of this paper improving its presentation. A version of this paper was presented in 1995 at the IBM T. J. Watson Research Center on kind invitation of the Mathematical Science department. This research has been made possible by the Netherlands Organization for Scientific Research (NWO) as part of the “Music, Mind, Machine” project.
References
Allen, J. F., and Ferguson, G. (1994) Actions and Events in Interval Temporal Logic. Journal of Logic and Computation, 4(5): 531-579.
Anderson, D. P. and Kuivila, R. (1990) A System for Computer Music Performance. ACM Transactions on Computer Systems, 8(1): 56-82.
Ashley, R. (1996) Aspects of Expressive Timing in Jazz Ballad Performance. Proceedings of the International Conference on Music Perception and Cognition. 485-490.
Benthem, J. van (1991) The Logic of Time (Synthese Library, vol. 156). Reidel: Dordrecht.
Bilmes, J. (1993) A Model for Musical Rhythm. Proceedings of the International Computer Music Conference, 207-210.
Cemgil A.T., Kappen, B., Desain, P. and Honing, H. (2001) On Tempo Tracking: Tempogram Representation and Kalman filtering. Journal of New Music Research.
Clarke, E.F. (1999) Rhythm and Timing in Music. In Deutsch, D. (ed.), Psychology of Music, 2nd edition. New York: Academic Press.
Clynes, M. (1995). Microstructural Musical Linguistics: Composer’s pulses are liked best by the best musicians, Cognition (International Journal of Cognitive Science), 55, 269-310.
Dannenberg, R. B. (1993) Music Representation: Issues, Techniques, and Systems. Computer Music Journal, 17(3), 20-30.
Dannenberg, R. B. (1997) Abstract Time Warping of Compound Events and Signals. Computer Music Journal, 21(3), 61-70.
Dannenberg, R. B., Desain, P., and Honing, H. (1997). Programming Language Design for Music. In G. De Poli, A. Picialli, S. T. Pope, and C. Roads (eds.), Musical Signal Processing. 271-315. Lisse: Swets and Zeitlinger.
Desain, P. and Honing, H. (1999) Computational Models of Beat Induction: The Rule-Based Approach. Journal of New Music Research, 28(1), 29-42.
Desain, P., and Honing, H. (1991) Tempo curves considered harmful. A critical review of the representation of timing in computer music. Proceedings of the International Computer Music Conference, 143-149.
Desain, P., and Honing, H. (1992). Time Functions Function Best as Functions of Multiple Times. Computer Music Journal, 16(2), 17-34.
Desain, P., and Honing, H. (1993). Tempo Curves Considered Harmful. In “Time in Contemporary Musical Thought” J. D. Kramer (ed.), Contemporary Music Review, 7(2). 123-138.
Desain, P., and Honing, H. (1994). Does Expressive Timing in Music Performance Scale Proportionally with Tempo? Psychological Research, 56, 285-292.
Desain, P., and Honing, H. (1996) Physical motion as a metaphor for timing in music: the final ritard. Proceedings of the International Computer Music Conference. 458-460.
Desain, P., Honing, H., Thienen, H. van, and Windsor, W. L. (1998) Computational Modeling of Music Cognition: Problem or Solution? Music Perception, 151-166.
Friberg, A. and Sundberg, J. (1999) Does music performance allude to locomotion? A model of final ritardandi derived from measurements of stopping runners. Journal of the Acoustical Society of America. 105(3), 1469-1484.
Gabrielsson, A. (1999) Music Performance. In Deutsch, D. (ed.), Psychology of Music, 2nd edition. New York: Academic Press.
Honing, H. (1993). Issues in the Representation of Time and Structure in Music. Contemporary Music Review, 9, 221-239.
Honing, H. (1995). The Vibrato Problem: Comparing Two Solutions. Computer Music Journal, 19(3) 32-49.
Jaffe, D. (1985) Ensemble Timing in Computer Music. Computer Music Journal, 9(4): 38-48.
Marsden, A. (2000) Representing Music Time. A Temporal-Logic Approach. Lisse: Swets and Zeitlinger.
McDermott, D.V. (1982) A Temporal Logic for Reasoning about Processes and Plans. Cognitive Science, 6.
Palmer, C. (1997) Music Performance. Annual Review of Psychology, 48, 115-138.
Repp, B. H. (1992). Probing the Cognitive Representation of Musical Time: Structural Constraints on the Perception of Timing Perturbations. Cognition (International Journal of Cognitive Science), 44, 241-281.
Roads, C. (1996) The Computer Music Tutorial. Cambridge: MIT Press.
Rogers, J., Rockstroh, J. and Batstone, P (1980) Music-Time and Clock-Time Similarities under Tempo Changes. Proceedings of the International Computer Music Conference, 404-442.
Scheirer, E. D. (1998) Tempo and beat analysis of acoustic musical signals. Journal of the Acoustical Society of America, 103(1), 588-601.
Steele, G. L. (1990). Common Lisp, the Language. Second Edition. Bedford, MA: Digital Press.
Sundberg, J. (1988) Computer Synthesis of Music Performance. In J. Sloboda (ed), Generative processes in Music: The Psychology of Performance. 52-69. Oxford: Clarendon.
Todd, N. P. M. (1992) The Dynamics of Dynamics: a Model of Musical Expression. Journal of the Acoustical Society of America, 91(6), 3540-3550.
Todd, N. P. M. (1999) Motion in Music: A Neurobiological Perspective. Music Perception. 17(1), 115-126.
[end of paper]