Henkjan Honing
[Published as: Honing, H. (1993). Issues in the representation of time and structure in music. Contemporary Music Review, 9, 221-239.]
This article describes a number of important issues in the representation of music with respect to the structuring of musical information. The set of issues presented is in no way complete, but indicates the most influential decisions that have to be taken in the representation of structure. The identification of the problems is central and there will be no speculation on possible solutions. The discussion will be restricted to the descriptive issues of music representation, concentrating on its primitives and their structuring. Of course, a purely technical description of a representation of music is not sufficient; its cognitive aspects should be incorporated as well. Although a discussion on the modeling of the "musical mind" is not the aim here, a cognitive viewpoint will add an essential perspective in the identification of the issues in the design of a general representation of music. Since a representation of the real world (represented world) has to do with cognition, the image (representing world) will have most of cognition's characteristics.
In the cognitive sciences, and in particular subfields like computational psychology and artificial intelligence, the use of computational models (or representational systems) is central. Their merits, together with the proposal of the term "cognitive science", were described by Christopher Longuet-Higgins as:
[...] it sets new standards of precision and detail in the formulation of models of cognitive processes, these models being open to direct and immediate test. (Longuet-Higgins, 1973)
The hope is that these formulations will contribute to a new theoretical psychology. Apart from the discussion whether a computational psychology is possible at all, a computational theory sets an important foundation: by describing a theory in terms of a formal system, together with its interpretation, it can be used to define what is faulty or inadequate (i.e. it can be falsified) and might help us in defining what kind of theoretical power we actually need. Or, as Margaret Boden states:
It provides a standard of rigour and completeness to which theoretical explanations should aspire (which is not to say that a program in itself is a theory). (Boden, 1990, p. 108)
Representation is an essential part of such a formal system and decisions made in its design will undoubtedly influence the behavior of the computational model, embodying the theory. It is these decisions, to be made with regard to a representational system of music, that this article is aiming at.
A number of different areas of research have a direct interest in specifying an appropriate representation of music. The latter either forms the basis of their studies or is a subject of study in itself. In the following short overview the different viewpoints and their specific demands will be described. The main difference is contained in the distinction between representations of a technical nature and representations of a cognitive nature (conceptual or mental representations).
Notation has always played a central role in musicological research. The design and adaptation of notations or representations have been developed along with the specific theories of analysis. Different overlapping or contradicting theories have been proposed (Schenker, 1956; Meyer, 1973; Narmour, 1977; Lerdahl & Jackendoff, 1983). Most theories agree that there is more in music than what is written in the score. In this sense, the opinion of the philosopher Nelson Goodman (1968) that a piece can be characterized as the set of performances in conformance with its score is an exception. The question here is whether a piece of music resides in the notation, in the air, or in people's minds, or in other words, whether music is cognitive or not.
In the field of computer music there is an interest in the design of appropriate data structures for music systems that form the basis of , for example, composition tools, interactive systems, and notation systems. Several projects have proposed different kinds of representation, suited to the specific demands of the particular problem or even to the software or hardware used (see Loy, 1988 for an elaborate survey of computer music systems). A distinction can be made between representations designed for real-time systems that are process-oriented (e.g. Puckette, 1988), and non-real-time systems that have a static global view of the music (e.g. Dannenberg, 1989). They differ,respectively, in their tacit and explicit representation of time (see below: The representation of time).
All systems have their own way of representing music and share little common ground. The only widespread standard is the industry proposed MIDI standard: a communication protocol (described in Loy, 1985) and file format. It is a very low-level stream-like and structureless representation (criticized in Moore, 1988) designed for communication between electronic instruments and computers. Within the computer music community several initiatives (Dannenberg et al, 1989; ANSI, 1989) have been taken towards a more general and high-level representational standard.
In music archiving the need for the standardization of notated music has resulted in several proposals for the storage and printing of music (Erickson, 1975; Byrd, 1984; Gourlay, 1986). Most of them are based on a visual description (e.g. notes positioned on staves) and are not very general in their applicability. The ANSI standardization committee for music representation (ANSI, 1989) is a recent attempt to make a technical and methodological specification for a standard music description language, useful in areas such as music publishing, music databases, computer assisted instruction, music analysis, and music production. In general, these standards seem to concentrate more on pragmatics (e.g. efficiency, in terms of size and speed requirements) than on generality and consistency.
Another large area of research is artificial intelligence (AI) and the cognitive sciences. Both have their own specific goals and demands. I will describe them here briefly.
In AI the concern is to notate descriptions of the world in such a way that an intelligent machine can come to conclusions about its environment by formally manipulating these descriptions. In knowledge representation, a subfield of AI, research is focussed on the development of representation languages and the design of inference schemes (e.g. to model reasoning about knowledge). Both are based in the tradition of (predicate) logic while more recent languages can be classified as structured object representations (e.g. frames; Minsky, 1975), associational representations (e.g. semantic networks; Quillian, 1968), and procedural representations and production systems (Newell, 1973). It is important to note that AI and knowledge representation are about feasible ways to build intelligent systems and not so much about modeling cognitive behavior.
AI and music is also an important field of research where representation is becoming one of the central issues (Balaban et al., 1991).
In the cognitive sciences, mental and knowledge representations are important subjects of study. It seems impossible to imagine a cognitive system in which a representation does not play a central role (Anderson, 1983; Fodor, 1983; Johnson-Laird, 1983). There is, however, no general agreement on the assumption that mental activity is mediated by internal or mental representations, and when there is, there is still some discord on the precise nature of these representations. Proposals for knowledge representation can be grouped into three categories: propositional representations (discrete symbols or propositions), analogical representations (use of images), and procedural representations (i.e. modeled as processes or procedures). To this last category also belong distributed representations (e.g. connectionist networks).
In the psychology of music, alongside research in music production and comprehension, the majority of work has consisted of describing the nature of musical knowledge and its representation. Elaborate studies have been done in the domains of pitch (Krumhansl, 1979; Shepard, 1982), rhythm (Povel & Essens, 1981; Longuet-Higgins & Lee, 1984; Desain & Honing, 1989) and timbre (Grey, 1977; Wessel, 1979). But here also, there is no general agreement on the precise nature of these representations (see McAdams, 1987 for a more complete overview or Sloboda, 1985; Dowling & Harwood, 1986).
This paragraph will outline the main approaches to representation. Identifying the problems of representation in general will be shown to be of direct benefit to the debate concerning music representation.
An important assumption in a formalist approach to representation is the knowledge representation hypothesis . It is summarized by Brian C. Smith (1982) as follows:
Any mechanically embodied intelligent process will be comprised of structural ingredients that a) we as external observers naturally take to represent a propositional account of the knowledge that the overall process exhibits, and b) independent of such external semantical attribution play a formal but causal and essential role in engendering the behavior that manifests that knowledge.
Such a "mechanically embodied intelligent process" is presumed to be an internal process that manipulates a set of representational structures, in such way that the intelligent behavior of the whole results from the interaction of parts. It is presumed only to react to the form or shape of these representations, without regard to what they mean or represent.
As an illustrative example one can use a technique that is sometimes used in making enlarged copies of pictures, for instance, by artists who make large chalk drawings of well-known paintings on the street. They copy these paintings from a small reproduction, holding the it upside-down. This minimizes the distorting influence a perspective has on the copying of the actual proportions: an unwanted interpretation that imposes `meaning' not present in the picture. This example shows that one has to watch out for interpretive knowledge, so easily added by human observers, not present in the representation itself. A representation is only syntax and should have all knowledge embodied in this syntax, independent of the interpretive system.
A representational system can be defined as "a formal system for making explicit certain entities or types of information, together with a specification of how the system does this" (Marr, 1982). In the formalist definition entities in a formal system might have complex mechanisms.[1] In deciding on any particular representational system and its entities, there is a trade-off; certain information will become explicit at the expense of other information being pushed into the background making it possibly hard to recover.
There is a classic distinction between declarative and procedural ways of representing knowledge: declarative being the knowledge about something, while procedural knowledge states the knowledge in terms of how to do something. Declarative knowledge tends to be accessible: it can easily be examined and combined. Procedural knowledge tends to be inaccessible, guiding a series of actions but allowing little examination. We seem to have conscious access to declarative knowledge whereas we do not have this access to procedural knowledge (Rumelhart & Norman, 1985).
Declarative representations have the merit of being composable i.e. the meaning of a complex expression is based on or can be derived from the meaning of its parts and their combinations. There are no interactions between separate entities, which makes the representation extremely modular. Knowledge can simply be added as long as it keeps the system consistent. All knowledge is open for introspection.
In procedural representations the emphasis is on interaction. Procedural representations are, not surprisingly, very powerful in modeling knowledge that is procedural by nature. There is no separation between facts and processes. Interactions are strong but deriving semantics is very hard (if not impossible). Addition or change is only reached by modification (and a resulting debugging process). Introspection and reflection is impossible. The problem, here, is the way in which procedures can be represented so that they can be interpreted. The question becomes what they do, instead of how they do it (see Table 1 for an overview).
Declarative knowledge Procedural knowledge
accessible inaccessible
modular (no interaction) interaction (no separation between
facts and processes)
composable semantics impossible (or hard) to derive
semantics
open to introspection and closed to introspection and
reflection reflection
knowledge can easily be added, if addition only by modification
consistent
control structure obscure control structure explicit
Table 1. Procedural and declarative knowledge representations compared.
In general, the distinctions between procedural and declarative representations are about efficiency, control , modularity, and the accessibility of knowledge. For computer science the first two are most important, while cognitive psychology is most interested in the last two.
Terry Winograd (1975) emphasized the duality between modularity and interaction, interaction being a strong characteristic of procedural representations and modularity of declarative representations. Many complex systems can be viewed as "nearly decomposable systems", a notion introduced by Herbert Simon (1969).[2] A single module can be studied separately without constant attention to its interaction(s) with other modules. Interactions among these subsystems are weak but not negligible. In representational terms, this forces us to have representations that facilitate these weak interactions. Mixed representations (i.e. both modular and interactive), as described by Winograd and others, have been further developed in the design of object-oriented languages (e.g. Minsky, 1975; Hewitt, 1975). In mixed representations different parts of the represented world are described in different ways. Some parts might be described procedurally, while others are described in a declarative way.
Another approach is to have multiple representations of the same `world', each describing the represented world completely. Instead of a mixture of, for example, procedural and declarative representations, describing different parts of the world, there is a procedural representation describing the whole world and a declarative representation describing the whole world in parallel. Here the trade-off is extra power against the problem of coordinating the information in the separate representations: when a change is made, all structures have to be kept consistent so as to reflect the same represented world.
The remainder of this article will address issues specific to the representation of music. Three sub-areas will be discussed: the primitives of a music representation, time structuring and general structuring. The notion of structuring depends on the possibility of decomposing a representation into meaningful entities, so we must first answer the important question: what are we structuring?
How to decompose a representation of music into the appropiate parts? What are the building blocks, the primitives of such a representation? As described earlier, this decision is essential and has implications on what kind of information will be lost and what information will clearly be represented.
There seems to be a general consensus on the notion of discrete elements (e.g. notes, sound events or objects) as the primitives of music. It forms the basis of a vast amount of music-theoretical work and research in the psychology of music, but a detailed discussion and argument for this assumption is missing from the literature. In music theory, as Robert Erickson (1982, p. 533) points out, there is no clear definition of what such a primitive object might be. In the psychology of music, John Sloboda (1985, p. 24), for example, just states "the basis phoneme of music is a note", and Diana Deutsch (1982) founds her discussion on grouping mechanisms in music on a `given' set of basic acoustic elements. Yet the essential question of what these elements or `phonemes' are is not answered. Research in psycho-acoustics on streaming shows how difficult it is to decide on such elements from a perceptual point of view (McAdams & Bregman, 1979; Bregman, 1990). A distinction has to be made between natural and artificial discretization of dimensions, or, in other words, the existence of possibly innate perceptual mechanisms and a learned division of continuous signals. In going from a continuous acoustic signal to a discrete signal one loses information. This quantization process should be looked at as a separation process instead: both types of information, the continuous and the discrete, are needed, and probably interact with each other (cf. Desain & Honing, 1989, with regard to this separation process in rhythm perception). So, next to decomposition, the issue of the characterization of the primitives of a representation, as continuous, discrete or a combination of the two, is very important.
By way of illustration, imagine Billie Holiday singing "I cried for you." How can the sound be represented in such a way that all expressive and structural information is incorporated? What is the relation between the actual perception and the notes originally notated in the score? Consists the sentence as sung of several discrete entities, or should it be described in a continuous way? Or a combination of both? For example, discrete phonemes, syllables or notes, continuous expression over these discrete structural elements, continuous fluctuations of pitch and amplitude within them, etc. combined into several levels of discrete and continuous types of information that are closely related.
In music cognition, the assumption of discrete elements finds a lot of support (McAdams, 1989). Stephen McAdams makes a distinction between three auditory grouping processes that organize the acoustic surface into musical events, connect events into musical streams, and `chunk' event streams into musical units (simultaneous, sequential and segmentational grouping, respectively); and perceived discrete qualities that are based on learning (e.g. scale, meter, harmony) (McAdams, 1989, p. 182). These discrete elements of music are assumed to carry structure, while the continuous aspects carry expression (Clarke, 1987). Mary Louise Serafine (1988) stands quite alone in arguing for a continuous basis. She blames music perception research for reducing music to false elements such as discrete pitches, scales and chords: "[they] are not the elements or building blocks of music" (p. 52). She accounts for these elements as an after-the-fact notion of music. But, as David Huron (1990) observes, these are speculative claims with no empirical support. It is clear that there is still quite a lot of discussion and research needed, especially on the rules of the segregation of acoustic signals, before we can decide on the discrete elements of a general representation of music.
Currently, most music representation systems use either notes or sound events/objects as the building blocks of their descriptions. In these systems, the distinction between continuous and discrete is normally between sound generation and the discrete events which describe the sound in several attributes, or, in other words, between the instrument and the score. This division rests on the assumption that sound is continuous by nature (e.g. signals, wave forms), whereas the score is mainly a collection of discrete events.The continuous aspects of the score (e.g. timing and dynamics) are often taken care of by different kinds of procedures or `modifiers' (e.g. Pope, 1989; Dyer, 1990) acting on the score: their descriptions are not part of the score representation (see below: Granularity). The trade-off made in these decompositions is very little discussed or even acknowledged.
When we have decided on the primitives of the representation, their structuring becomes of great importance. This structuring will be described in two separate sections. Since time and its structuring is an important factor in music, with its own specific issues related to it, it will be discussed separately from the issues in general structuring. However, in the end it will be shown that they are not very different. Time structuring will be discussed first.
A number of distinctions need to be made in trying to narrow down discussion of the representation of time. There are three different areas of interest: temporal representation, temporal logic or reasoning, and planning and scheduling. All of them influence the design of a representation of time. This section will concentrate on the first.
The representation of time can be subdivided in three categories: 1) tacit (time is not represented at all); 2) implicit (time is represented, but explicit time relations are not); and 3) explicit (time is represented with explicit time relations). The issues will be spread over these categories.
Some real-time systems can be called `no-time' systems (e.g. Bharucha,1987; Puckette, 1988). Because time is not explicitly represented in the primitives, there is only the notion of now. There is no explicit formulation of the systems dependence on time and no information regarding time (except `now') can be derived or manipulated.
In this category, time is represented without explicit time relations. Time is expressed in an absolute way (e.g. note lists (Matthews, 1969)) or relative to an arbitrary point of reference. Time relations (e.g. this note occurs before that note, or, these notes are overlapping) have to be calculated since they are not explicitly stated in the representation.
The decision to represent time as points or intervals is not arbitrary, even when they, theoretically, can be expressed in terms of each other (an interval is a collection of points, a point is a very short interval[3]). A point-based representation (McDermott, 1982) implies the occurrence of only one event at a time and lacks the concept of an event `taking' time. As Allen (1983) argues, there seems to be a strong intuition that, given an event, we can always "turn up the magnification" and look at its structure. He therefore proposes an interval-based representation. Intervals form a strong basis for the computability of meaningful relations, i.e. time intervals that overlap, meet, are during, before, and after each other, etc.
In music representation there are examples of both choices. Mira Balaban (1989), for instance, describes a representation based on pairs of a sound object and a time point, and Desain & Honing (1988) use sound objects with a duration (i.e. time interval) as the basis of a representation of time.
The time base that can be chosen is either absolute or relative, or, in other words, real-time (e.g. in seconds) or proportional time (e.g. a quarter note). With an absolute time base, (onset-)time is an attribute of the musical object, whereas with a relative time base it isn't.
Some music representation systems (Smith,1972; Schottstaedt, 1983) use lists of notes with absolute times, whereas later systems tend to describe time in terms of a relative time base or relative to the enclosing time context, i.e. expressed as a function of this context (Dannenberg, 1989; Balaban, 1989). But both time bases seem to be needed. For example, in representing a trill as being twice as long as another trill, one has to decide whether to stretch or to extend the description of this related trill, i.e. is the new trill half the speed (using relative time) or is the speed the same (using absolute time) and are there just more notes added (or any other particular way of extending a trill). Both types of behavior, using both time bases, need to be represented to allow for both representations of time.
What is the grain or grid size of the time bases mentioned above? Is time expressed as a discrete value labeling events, or is it expressed as a continuous function? As well as discrete time, a continuous way of representing time is needed, for example, when representing an accelerando or rubato over a series of notes.[4] Most representational systems make these notions available as global operations acting upon the representation instead of making them part of the representation.
An example of explicit time structuring in music is the use of two basic structuring relations called `parallel' and `sequential' (Desain & Honing, 1988). These two time relations, and combinations of them, can express many constellations of discrete sound events. Similar time structuring is proposed by several other authors (e.g. Rodet & Cointe, 1984; Dannenberg, 1989). Allen (1983) describes a list of thirteen possible relationships. A set of basic explicit time relations forms a solid basis for higher level notions of time structuring and make operations on time, or operations depending on time, very elegant (Desain, 1990).
The controversy over declarative and procedural representations is also very important in the representation of music. Take the example of a trill - a sequence of notes, alternating in pitch, filling up a certain time interval. This "filling up" is most naturally represented in a procedural form. But, as discussed previously, this type of representation has quite some disadvantages. Problems occur when there is, for instance, a nesting of these trills defined in terms of each other (e.g. a higher-level trill composed by combining the definitions of some other, i.e. lower-level trills): the definition of the high-level trill depends on the result of the low-level trills, a result that is only available after execution of the procedural description of these low-level trills. There is no way in which the duration of the high-level trill can be decided upon without evaluating the definition of the low-level trills since this knowledge is represented in a procedural form. The declarative representation (a low-level trill of a certain length) has to be replaced by the result (a sequence of notes adding up to a certain length) and information is lost (e.g. knowledge on how the trill was composed). Both kinds of representation seem to be needed in the representation of music. The marriage of both types of knowledge is, as described before, still a topic of research.
Structural descriptions of music can be divided into two areas. One is the description of musical structure independent of psychological considerations, based on an analysis by a musicologist. The other is the description of the structural properties of mental representations of music: the goal of music psychology research. The described issues are relevant to both areas. In describing general structuring, we can employ the same division used in the subfield of time structuring: 1) tacit structural relations, 2) implicit structural relations, and 3) explicit structural relations.
When no structure is represented, we are left with only the primitives of the representation. This is the case in the earlier mentioned MIDI protocol that represents a piece of music as a structureless stream of note-onsets and offsets (with as attributes an integer key number, a velocity value and channel number).
Implicit are those structural relations that have to be calculated from the representation. As an example, from a MIDI file format the following structural information can be obtained: all notes on channel 1 belong to one unit called a `track'; every two seconds there is a bar and all notes within that time span are part of it; etc. The structural relations that can be derived from a representation (with only implicit structuring) depend heavily on the choice of primitives and their attributes.
Structure is the denominator for a large class of possible relations made between the entities of a representation. One can say that almost everything, except the entities themselves, is structure. Very few representational systems for music supply explicit structuring mechanisms, and even when they are available, they only represent specific kinds of structure (e.g. meter, bars, instrumental parts) or support annotation (e.g. "this is an important note"). The following paragraphs discuss the issues in the design of a general structuring mechanism.
One way of describing different kinds of relations -so as to have a handle to talk about them in a general way- is to divide them in binary and n-ary relations. A special kind of binary relation is a tree or hierarchy. A part-of relation defines such a hierarchical relation between objects. It propagates behavior between objects. A part-of relation could denote relations such as "all notes part-of chord", or the often-used bar, beat, and note hierarchy. They are quite general and flexible in describing musical structure (see Honing, 1990).
Another hierarchical relation, orthogonal to the part-of relation, is the is-a relation. It defines inheritance of behavior and characteristics, specifying a generalization hierarchy of objects: a structure of concepts which are linked to those of which they are specializations. Examples are: a dominant chord being a special kind of seventh chord, a chord being a kind of cluster, a cluster being a kind of collection of notes, etc. (see e.g. Pope, 1989).
A great number of music theories use hierarchies as their only kind of structuring (Lerdahl & Jackendoff, 1983). Hierarchies are very useful in relating local and global information, but other kinds of relations are needed as well. Other binary relations like associative relations are useful in relating, for example, a theme with its variations. Functional relations are also needed (e.g. the function of a particular chord in a scale) as well as referential relations (e.g. a theme referring to a previously presented or already known motif).
N-ary relations can structure more complex types of relation: for instance, the dependency of a certain chord on scale, mode and the context in which it is used is a ternary relation.
The structural types described here are the ones most relevant to music, though a complete overview of all musical constructs and their expression in these structural types would take considerably more space.[5]
Not everything is said about musical structure by simply assigning one of the structural types described above. Within one type of structure (e.g. defined in terms of part-of relations) refinement is needed to distinguish between the different musical constructs described by means of this type (e.g. what is the difference between a chord and a bar when both are described in terms of part-of relations?). There are two extremes in approaching this problem. One approach is dedication: all the well-known or often used musical constructs (chord, arpeggio, bar, beat, trill, grace note, etc.) are described, more or less ad hoc, as primitives with their own specific relations (and resulting behavior), with little or no hierarchy. The other approach is generalization and is based on parsimony: there are no special musical constructs defined as primitives, all constructs being based on some very general primitive (e.g. a time interval). The bias is on generality: new musical constructs have to be defined in terms of existing ones, in a hierarchical way.
The first is a popular and pragmatic approach. For instance, in a computer composition system a reasonable set can be provided that takes cares of most needs. The main drawback is that extensions have to be made in an ad hoc fashion and often need to have their own processes (or transformations) defined for the user to be able to access or manipulate them.
In the latter approach the choice of the right generalities is the problem. But when they are available, extensions are simply defined in terms of these generalities or higher-level constructs. There is no need to `tell' the processes, acting on the representation, about these new constructs.
In expressing one of the above mentioned relations, it is important to note how the information flow is supported by the representation. In music theory and the psychology of music, different directions are proposed: from the conceptual level down (top-down; Schenker, 1956), and from the low-level data up (bottom-up; Narmour, 1977), or in both directions, as in modeling tonal hierarchies with interactive activation networks (Bharucha, 1987).
In what way is musical structure different from any general structure mechanism (e.g. the part-of and is-a relations we described before)? Since time is an influential factor in most, if not all types of structure in music, musical structure can be described as a collection of structuring mechanisms that have time intervals associated with their components (i.e. structural objects). It is the constraints on these time intervals that specialize the different types of structuring.
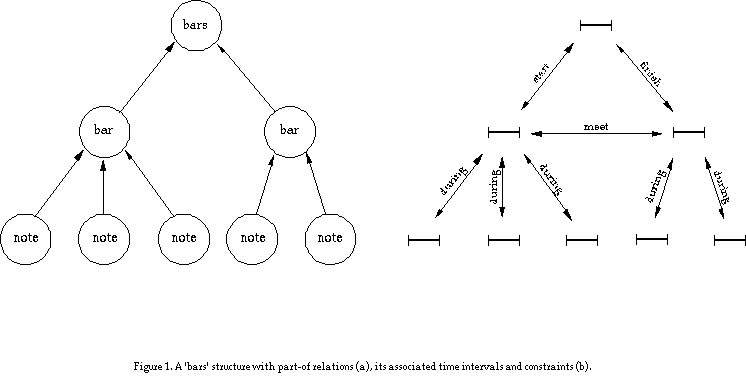
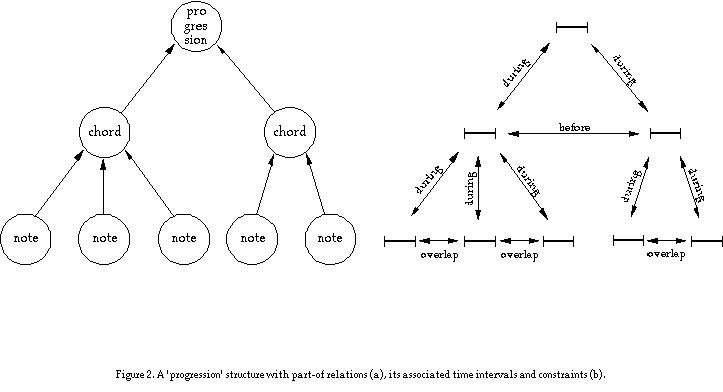
As an example, let's look at two simple part-of relations: bars, a bar, note (see Figure 1a), and a progression, chord, note hierarchy (see Figure 2a). In the first hierarchy it is clear that the structural object `bars' and its parts have a duration: they hold for a certain time interval. This is also the case for the `progression' object and its parts. Both constructs have the same part-of structure but differ in the kind of constraints they have on their associated time intervals. In a `bars' structure, if one bar becomes longer, the other one has to become shorter: they have to satisfy the meet constraint (using Allen's (1983) terminology). In the 'progression' structure, the comparable structural objects have a before relation. The musical constructs are characterized by the specific constraints on these time intervals associated with their structural objects (see Figure 1b and 2b)[6].
These constraints should be part of the representation, i.e. part of the syntax, so that operations on the representation produce the behavior resulting from these restrictions for free; the semantics of musical constructs (e.g. what does an arpeggio mean, and how does it differ from a chord or a run of notes) should be moved to the syntax. In this way the representation has embedded knowledge of how to deal with particular kinds of structure. These musical constructs can be compared with small machines: they have a clear and accessible behavior that cannot be altered.

Multiple representations are needed in a complete description of music, i.e. several structural descriptions being applied to the same primitives (e.g. a note is part of a meter and a tonal hierarchy at the same time). One could think of multiple structural representations as analogous to a ring binder: the spiral resembles the primitives, the pages the different kinds of structural relations.[7] As described before (see General approaches to representation), the consistency and coordination of the information between the pages is the problem here.
Inconsistencies may occur when two structural descriptions clash (i.e. the constraints on both structural descriptions can't be solved or unified) and exceptional or preferred behavior has to be provided. It seems that in these situations, the demand for consistency is too strong (e.g. a slowed-down chord structure might turn into an arpeggio). It may not be possible to formalize a representation of music in a way that guarantees consistency.[8] More research is needed in the formalization of musical constructs (i.e. definition and behavior) and their combination that might result in exceptional or preferred behavior.
Here the issue is whether structuring is used to add musical knowledge or just used as annotation. Structure can be used as an annotation of the basic elements of the representation assigning different kinds of information, but it can also be interpreted as musical knowledge. Using structure in both ways facilitates modularity: not all knowledge about music has to be part of the representation, since structure can be used as a hook to import information from outside the system. This improves the modularity of the system considerably (as advocated by Simon (1969) in technical terms, and by Fodor (1983) in cognitive terms).
Representational systems have a central position in the cognitive sciences, especially in the fields of computational psychology and artificial intelligence. A formalist approach to representation, as summarized in the "knowledge representation hypothesis", applied to the representation of music has turned out to be beneficial. Representing musical knowledge in syntactical terms, makes a theory within the psychology of music explicit and verifiable. Discussing the issues in the design of such a representational system for music is what this article has aimed at.
Before talking about structuring, the question "what are we structuring ?" was asked. The decomposability of a representation of music was discussed as well as the expression of its primitives in either discrete or continuous terms (or a combination thereof). Research in the segregation of acoustical signals (Bregman, 1990) is essential in deciding on the primitives of a general representation of music. Currently, most research is based on the assumption that the basic elements of music are discrete.
The discussion of time structuring, as a special case of general structuring, showed that the choice of either points or intervals, a relative or absolute time base, discrete or continuous representations, and the use of procedural or declarative descriptions of musical knowledge are controversies where solutions through combining these polarities have to be found.
Several types of general structuring were discussed. An important point is the observation that structure in music is often associated with a time interval (for which it `holds'). The constraints on these time intervals model specific musical constructs and their behavior. Time structuring and general structuring differ in the sense that time structuring makes these constraints explicit: they are represented as structural objects (e.g. `parallel' and `sequential' relations), while in general structuring they are implicit: they are used to restrict the behavior of the specific structure, but are not explicitly represented as structural objects.
In conclusion:
1) A representation should be as formal as possible. Even when the meaning is removed from the formal system it must be possible to prove its correctness (i.e. not dependent on knowledge outside the the formal definition).
2) A representation should be as declarative as possible. Declarative representations were shown to have preference over procedural representations, even though some information is more naturally represented in a procedural way.
3) A representation should be as explicit as possible. All relations and knowledge should be explicitly stated in the representation.
4) All the controversies presented above need combined solutions in which both extremes can be expressed. The idea of having multiple representations of the same `world' seems useful.
5) Musical structure should be associated with time intervals. Constraints on these time intervals model the specific musical constructs and their behavior. These constraints should be part of the representation, i.e. part of the syntax, so that operations on the representation get the behavior resulting from these restrictions for free.
In the short term, it is concluded that it would be best to construct representations of msuic so as to be as declarative, explicit and formal as possible, while actively awaiting developments in representation languages or schemes that can deal with the issues presented here in a more flexible way. [9]
Thanks to David Huron, Christopher Longuet-Higgins, Steve McAdams, Stephen Pope, Maria Ramos, and my colleagues at City University, Music Department and the Centre for Knowledge Technology for useful discussions and advice. Special support by Johan den Biggelaar, Ton Hokken and Thera Jonker is highly appreciated. Thanks for proof-reading and valuable suggestions and improvements on earlier versions to Eric Clarke, Joop Ringelberg, and an anonymous referee. The research was in part supported by an ESRC grant under number A413254004. Finally, special thanks to Peter Desain for his encouragement, insights, and generous sharing of ideas.
Allen, J.F. (1983) Maintaining Knowledge about Temporal Intervals. In: Communications of the ACM, 26(11).
Anderson, J.R. (1983) The Architecture of Cognition. Cambridge, Mass.: Harvard University Press.
ANSI (American National Standards Institute) (1989) X3V1.8M/SD-6 Journal of Development Standard Music Description Language (SMDL). San Francisco: Computer Music Association.
Balaban, M. (1989) Music Structures: A Temporal-Hierarchical Representation for Music. Musikometrika, Vol. 2.
Balaban,M., K. Ebcioglu & O. Laske, eds (1991) Musical Intelligence. Menlo Park: The AAAI Press. (forthcoming ).
Bharucha, J.J. (1987) MUSACT: A Connectionist Model of Musical Harmony. In Proceedings of the Cognitive Science Society. Hilsdale, New Jersey: Erlbaum.
Boden, M. A. (1990) Has AI helped psychology? In: The foundations of artificial intelligence. A source book, edited by D. Partridge and Y. Wilks. Cambridge: Cambridge University Press.
Bregman, A.S. (1990) Auditory Scene Analysis: The Perceptual Organization of Sound. Cambridge, Mass.: Bradford books, MIT Press.
Byrd, D. (1984) Music Notation by Computer. Ph. D. Dissertation, Computer Science Department, Indiana University. Ann Harbor: University Microfilms.
Clarke, E.F. (1987) Levels of structure in the organisation of musical time. In "Music and psychology: a mutual regard", edited by S. McAdams. Contemporary Music Review, 2(1).
Clarke, E.F. (1988) Generative principles in music performance. In Generative processes in music. The psychology of performance, improvisation and composition, edited by J. A. Sloboda. Oxford: Science Publications.
Dannenberg, R. (1989) The Canon Score Language. Computer Music Journal 13(1).
Dannenberg, R., L.M. Dyer, G.E. Garnett, S.T. Pope, & C. Roads (1989) Position papers. In Proceedings of the 1989 International Computer Music Conference. San Francisco: Computer Music Association.
Desain, P. & H. Honing (1988) LOCO: A Composition Microworld in Logo. Computer Music Journal 12(3).
Desain, P. & H. Honing. (1989) Quantization of Musical Time: A Connectionist Approach. Computer Music Journal 13(3). Reprinted and updated in Todd & Loy (1991).
Desain, P. & H. Honing. (1991a). Tempo curves considered harmful. In "Music and Time", edited by J. D. Kramer. Contemporary Music Review. London: Harwood Press. (forthcoming).
Desain, P. & H. Honing. (1991b). Towards a calculus for expressive timing in music. Research Report. Utrecht: Centre for Knowledge Technology.
Desain, P. & H. Honing. (in press) Time functions function best as functions of multiple times. To appear in Computer Music Journal.
Desain, P. (1990) Lisp as a second Language. Perspectives of New Music, 28(1).
Deutsch, D. (1982) Grouping Mechanisms in Music. In The Psychology of Music, edited by D. Deutsch. New York: Academic Press.
Dowling, W.J. & D. Harwood. (1986) Music Cognition. New York: Academic Press.
Dyer, L. (1990) Ensemble. Proceedings of the 1990 International Computer Music Conference. San Francisco: Computer Music Association.
Erickson, R. (1975) The DARMS Project: A Status Report. Computers and the Humanities, 9(6).
Erickson, R. (1982) New Music and Psychology. In The Psychology of Music, edited by D, Deutsch. New York: Academic Press.
Fodor, J. (1983) The Modularity of the Mind: An Essay on Faculty Psychology. Cambridge, Mass.: Bradford Books, MIT Press
Goodman, N. (1968) The Languages of Art: An Approach to a Theory of Symbols. Indianapolis: Bobbs-Merill Co.
Gourlay, J.S. (1986) A Language for Music Printing. Communications of the ACM, 29(5).
Grey, J.M. (1977) Multidimensional Perceptual Scaling of Musical Timbres. Journal of the Acoustical Society of America, 61.
Hewitt, C. (1975) How to use what you know. Proceedings of the Fourth International Joint Conference on Artificial Intelligence. Los Altos, CA.: Morgan Kaufmann.
Honing, H. (1990) POCO: An Environment for Analysing, Modifying, and Generating Expression in Music. Proceedings of the 1990 International Computer Music Conference. San Francisco: Computer Music Association.
Huron, D. (1990) Book review of Music as Cognition by M.L. Serafine. Psychology of Music, 18.
Johnson-Laird, P.N. (1983 ) Mental Models: Towards a Cognitive Science of Language, Inference, and Consciousness. Cambridge, Mass.: Harvard University Press.
Krumhansl, C.L. (1979) The Psychological Representation of Musical Pitch in a Tonal Context. Cognitive Psychology, 11.
Lerdahl, F. & R. Jackendoff (1983) A Generative Theory of Tonal Music. Cambridge, Mass.: MIT Press.
Longuet-Higgins, H.C (1973) Comments of the Lighthill Report. Artificial Intelligence - A Paper Symposium. London: Science Research Council. Reprinted in Longuet-Higgins (1987).
Longuet-Higgins, H.C (1987) Mental Processes. Cambridge, Mass.: MIT Press.
Longuet-Higgins, H.C. & C.S. Lee (1984) The Rhythmic Interpretation of Monophonic Music. Music Perception, 1. Reprinted in Longuet-Higgins (1987).
Loy, G. (1985) Musicians Make a Standard: The MIDI Phenomenon. Computer Music Journal 9(4). Reprinted in Roads (1989).
Loy, G. (1988) Composing with Computers - A Survey of Some Compositional Formalisms and Music Programming Languages. In Current Directions in Computer Music Research, edited by M. V. Matthews & J. R. Pierce. Cambridge, Mass.: MIT Press.
Marr, D. (1982) Vision: A Computational Investigation into Human Representation and Processing of Visual Information. San Francisco: W.H.Freeman.
Matthews, M.V. (1969) The Technology of Computer Music. Cambridge, Mass: MIT Press.
McAdams, S & A. Bregman (1979) Hearing Musical Streams. Computer Music Journal 3(4). Reprinted in Roads & Strawn (1985).
McAdams, S. (1987) Music: A Science of the Mind? In "Music and Psychology: A Mutual Regard", edited by S. McAdams. Contemporary Music Review, 2(1).
McAdams, S. (1989) Psychological constraints on form-bearing dimensions in music. In "Music and the cognitive sciences", edited by S. McAdams and I. Deliège. Contemporary Music Review, 4(1).
McDermott, D.V. (1982) A Temporal Logic for Reasoning about Processes and Plans. Cognitive Science, 6.
Meyer, L.B. (1973) Explaining Music: Essays and Explorations. Berkeley: University of California Press.
Minsky, M. (1975) A Framework for Representing Knowledge. In The Psychology of Computer Vision, edited by P. Winston. New York: McGraw-Hill.
Moore, F.R. (1988) The Dysfunctions of MIDI. Computer Music Journal 12(1).
Narmour, E. (1977) Beyond Schenkerism: The need for Alternatives in Music Analysis. Chicago: University of Chicago Press.
Newell, A. (1973) Productions systems: models of control structures. In Visual Information Processing, edited by W.G. Chase. New York: Academic Press.
Pope, S.T. (1989) Modeling Musical Structures as EventGenerators. Proceedings of the 1989 International Computer Music Conference. San Francisco: Computer Music Association.
Povel, D.J. & P. Essens (1981) Perception of temporal patterns. Music Perception, 2
Puckette, M. (1988) The Patcher. In Proceedings of the 1988 International Computer Music Conference. San Francisco: Computer Music Association.
Quillian, M.R. (1968) Semantic Memory. In Semantic Information Processing, edited by M.L. Minsky. Cambridge, Mass: MIT Press.
Roads, C (ed.) (1989) The Music Machine. Cambridge, Mass.: MIT Press.
Roads, C. & J. Strawn (eds.) (1985) Foundations of Computer Music. Cambridge, Mass.: MIT Press.
Rodet, X. and P. Cointe. (1984) FORMES: Composition and Scheduling of Processes. Computer Music Journal 8(3). Reprinted in Roads (1989).
Rumelhart, D.E. & D.A. Norman. (1985) Representation of Knowledge. In Issues in Cognitive Modeling, edited by A. M. Aitkenhead and J. M. Slack. London: Lawrence Erlbaum Ass.
Schenker, H. (1956) Der Freie Satz. Vienna: Universal Edition
Schottstaedt, W. (1983) PLA: A Composer's Idea of a Language. Computer Music Journal 7(1). Reprinted in Roads (1989).
Serafine, M.L. (1988) Music as Cognition: The Development of Thought in Sound. New York: Columbia University Press.
Shepard, R.N. (1982) Structural approximations of musical pitch. In The Psychology of Music, edited by D, Deutsch. New York: Academic Press.
Simon, H. (1969). The Architecture of Complexity. In The Sciences of the Artificial. Cambridge: MIT Press.
Sloboda, J. (1985) The Musical Mind: The Cognitive Psychology of Music. Oxford: Clarendon Press.
Smith, B. C. (1982) Reflection and Semantics in a Procedural Language. Ph.D. dissertation. Technical Report MIT/LCS/TR-272, Cambridge, Mass.: MIT.
Smith,L. (1972) SCORE - A Musician's Approach to Computer Music. Journal of the Audio Engineering Society, 20.
Todd, P.M. & D.G. Loy (Eds.) (1991) Music and Connectionism, Cambridge, Mass.: MIT Press.
Wessel,D. (1979) Timbre space as a musical control structure. Computer Music Journal 3(2).
Winograd, T. (1975) Frame Representations and the Declarative/Procedural Controversy. In Representation and Understanding: Studies in Cognitive Science, edited by D.G. Bobrow and A.M. Collins, New York: Academic Press.
[1] Distributed representations (e.g. connectionist networks), in this sense, manipulate symbols of an unusual kind. An individual unit of such network does not implement an identifiable symbol; a meaningful representation only exist at a level made up of a number of units.
[2] Simon (1969) describes nearly decomposable systems as having the property "the short-run behaviour of each of the component subsystems is approximately independent of the short-run behaviour of the other components" (p. 100).
[3] Allen's theory (1983), describes points as intervals that are durationless, i.e. a duration less than a value [[epsilon]], adjusted to the reasoning task.
[4] It has been shown that structure is essential in the performance of the continuous and discrete aspects of musical time (e.g. Clarke, 1987, 1988). Therefore a complete representation of time should facilitate the expression of these aspects in terms of structure to be of any perceptual or musical relevance (see Desain & Honing, 1991a).
[5] A complete overview of all musical constructs will quite likely turn out to be a large, if not infinite collection, but they probably can be grouped into a considerably smaller set of proto-typical relations, with their specific characteristics being modeled as refinements of a particular structural type (see issue on Musical structure: association with time intervals and their constraints essential).
[6] The constraints on the time intervals, as shown in Figure 1b and 2b, give a raw characterization of the example structures, just for comparison. For a more complete characterization of such structures the logic-based constraints of Allen (1983) are not enough. Other kinds of constraints are needed as well to be able to express relations like, for example, all bars have the same length, or, a bar is half the length of `bars'.
[7] These pages could be of different shapes and material, standing for structural descriptions of a completely different nature. This analogy was suggested by Morris Halle in a seminar at Sussex University in 1987 when talking about conceptual representations of linguistic structure.
[8] Recent work done in the field of artificial intelligence on non-monotonic logic and truth-maintenance might therefore be applicable to music.
[9]Since this article was written (autumn, 1990) work has been done on partial solutions of the issues presented above. Some of the issues on the representation of time have been resolved in a generalized concept of time functions (Desain & Honing, in press). A proposal for a specification and transformation formalism of expressive timing described in terms of structure is published as Desain & Honing (1991b).