This paper is a based on a study of

Deutsch, Diana, J. Feroe, The Internal Representation of Pitch Sequences in Tonal Music Psychological Review, 88 no. 6, pp. 503-522 (1981).

Claim: people memorize information hierarchically

Corollary: sequences of musical pitches are memorized hierarchically.

Question: what do hierarchical mental representations of musical pitches look like?

Deutsch and Feroe propose an answer to this question. Furthermore, they introduce a formalism to denote these representations.

This formalism is widely used in research in musical psychology, e.g in key recognition.

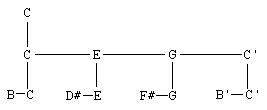
According to Deutsch and Feroe, the sequence
b c d# e f# g b' c' is represented as:

The hierarchical structure is clearly visible.

This tree is denoted by:

{{(*,n2,n2,n3);C-maj} [pr] {(p,*);Cr}; c}

Although the Deutsch and Feroe formalism is used widely, the formalism itself is usually taken for granted. However, many questions arise:

1) What is the exact relation between the trees and the expressions?

2) Which syntactical forms are allowed for the expressions?

3) Why is the proposed expression language so complex?

4) What is the semantics of an expression (trees? pitch sequences?)

In our work, we tried to answer these questions by applying well-known techniques from computing science, originally designed to define syntax and semantics of programming languages.

A language is a (often infinite) set of sentences. (A sentence is a string of symbols, drawn from an alphabet).

It is in general not possible to define this set by providing a finite number of examples. Languages can be defined by providing grammars.

The grammar also defines the syntactic structure of any sentence in the language.

In our case, a context free grammar is sufficient to formally define the set of all D&F expressions.

The hierarchical syntactical structure of a sentence can be represented by so-called parse trees.

Parse trees can be used to define the meaning of a sentence in terms of the meanings of the subparts (compositionality).

Context free grammars can be used as input to programs that generate syntactical analyzers and recognizers for the language.

It is useful to make a distinction between the "kernel language" and syntactic sugar (such as convenient abbreviations)

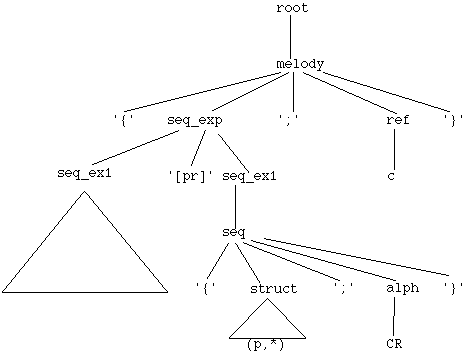
Example (excerpted from the full grammar)

root : melody

| seq_exp

...

;

melody : '{' seq_exp ';' ref '}'

| mel_var

;

seq_exp : seq_ex1 '[pr]' seq_ex1

| seq_ex1

;

seq_ex1 : seq

...

;

seq : '{' struct ';' alph '}'

...

| seq_var

;

struct : '(' oppref '*' opsuf ')'

| struct_var

;

Up to now, we have only defined the kernel language formally. Many of the syntactic suger concepts that occur in the paper will be added later.

The semantics of the language is defined in two steps:

1) We provide a syntax driven (compositional) way to derive the semantics of sentences in the kernel language in terms of so-called melo-trees. These melo-trees are defined formally as well.

2) For syntactic sugar concepts, we define formally how corresponding sentences in the kernel language can be constructed. The semantics of the sugar equals the semantics of the corresponding kernel sentence.

Conclusions

The formalism proposed by Deutsch and Feroe is useful and indeed often used.

However, it is difficult to apply, because its formal definition is insufficiently elaborated.

Fortunately, application of modern techniques from computing science can be used to fill in these gaps.

A set of tools has been built and is currently incorporated in the music analysis tool POCO.